C’est quoi le modèle Mundell-Flemming avec parfaite mobilité des capitaux ?
Rédacteur : Stéphane Ménia
Le modèle Mundell-Flemming (Robert Mundell, Marcus Flemming, début années 1960) est l’extension du modèle IS-LM en économie ouverte. Il partage avec lui la fixité des prix (hypothèse qui en réalité correspond surtout à dire que l’ajustement des prix des actifs financiers est plus rapide que celui des biens et services, qui peuvent donc être considérés comme fixes à court terme) et les grandes relations comportementales et d’équilibre (marché de la monnaie et marché des biens sont étudiés). On pourra donc se référer à IS-LM pour certaines explications, ignorées ou survolées ici.
Quand on introduit les marchés financiers internationaux, on peut raisonner sur une mobilité parfaite des capitaux ou une mobilité imparfaite. Dans le cas de mobilité imparfaite, les marchés financiers ne sont pas totalement intégrés et les mouvements de capitaux ne répondent pas instantanément aux variations des prix, notamment aux variations des taux d’intérêt ou taux de change. Cette présentation suppose une mobilité parfaite des capitaux, ce qui s’approche le plus de la situation d’un pays comme la France.
On suppose qu’on est dans le cas d’un petit pays, de sorte qu’il peut emprunter et prêter tant qu’il veut sur le marché mondial sans que cela n’ait d’influence sur le taux d’intérêt.
L’équilibre de l’économie
L’équilibre dans cette économie est résumé par trois équations :
Y = A(Y, i, G, T) + XN(e) (IS)
M = L(Y,i) (LM)
I = i* (BP)
A(Y, i, G, T) représente l’absorption et correspond à C + I + G – T dans la courbe IS classique.
XN(e) représente les exportations nettes (exportations – importations). Elles diminuent avec e (l’appréciation de e renchérit le prix des biens nationaux et réduit celui des biens importés).
M est la masse monétaire nominale, égale ici à la masse monétaire réelle M/P, sachant que, par commodité, puisque les prix sont fixes, on a posé P, le niveau général des prix, égal à 1.
e est le taux de change nominal. Il est égal au taux de change réel q = e P/P* où P* sont les prix mondiaux et ont été aussi fixés pour simplifier à 1. Une hausse de e traduit une appréciation de la monnaie.
La dernière équation (BP) traduit l’équilibre de la balance des paiements, quand on a mobilité parfaite des capitaux. Elle énonce que le taux d’intérêt national i est égal au taux d’intérêt mondial i*.
L’idée est la suivante, en raisonnant sur la zone euro : lorsque le taux d’intérêt européen est supérieur au taux d’intérêt mondial, il est plus intéressant pour les investisseurs étrangers d’investir dans la zone. Il y a donc des entrées de capitaux. Ces entrées de capitaux se traduisent par un échange de devises contre des euros. Cet échange se fait par la création d’euros par la Banque centrale européenne qui met en réserves les devises achetées.
La masse monétaire augmente, ce qui réduit le taux d’intérêt sur le marché de la monnaie et le ramène à son niveau antérieur. Les investisseurs se désintéressent des placements en euros et le phénomène inverse du mouvement initial apparaît : l’offre d’euros augmente et la BCE achète des euros avec des devises, ce qui réduit la masse monétaire et fait croître le taux d’intérêt jusqu’à son niveau initial, celui où le taux européen est égal au taux mondial (et où il n’y a donc plus de raison de modifier la localisation des investissements).
Notez en passant que l’hypothèse de la zone euro comme «petit pays ouvert» est fausse et juste retenue pour que le mécanisme soit parlant pour un lecteur français…
Conclusion d’étape logique : le taux d’intérêt d’un petit pays ouvert est fixé au niveau mondial. Ce qui aura une influence sur l’analyse des politiques économiques.
L’équilibre se représente graphiquement de la façon suivante.
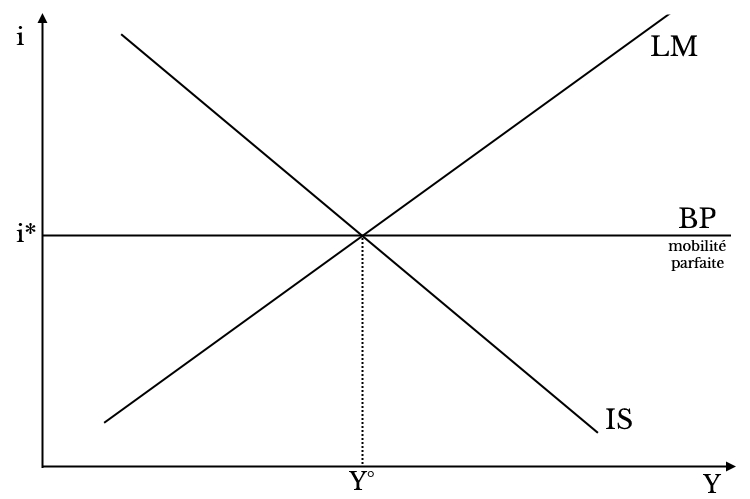
Les politiques économiques
Politiques économiques en change fixe
Principe et implication du change fixe
En change fixe, la banque centrale s’engage à maintenir le taux de change au même niveau.
Si l’offre de monnaie nationale sur le marché des changes dépasse la demande, un système de change flexible se traduirait par une baisse du prix de la monnaie nationale (une dépréciation).
En change fixe, la banque centrale empêche ce mouvement en demandant la monnaie nationale pour un montant correspondant à l’excès d’offre. Elle paie des devises en échange. La masse monétaire subit donc une contraction. La masse monétaire n’est pas contrôlée par la banque centrale, mais déterminée par le marché des changes.
L’offre de monnaie nationale est donc endogène.
Politique budgétaire en changes fixe
On suppose une hausse des dépenses publiques, G. Cette hausse stimule la demande A, ce qui accroît le revenu Y.
Sur le marché de la monnaie, la hausse de Y accroît la demande de monnaie et accroît le taux d’intérêt, comme en économie fermée. Mais cette hausse du taux d’intérêt n’est que temporaire. Elle induit une entrée de capitaux.
Cette entrée de capitaux pèse positivement sur le taux de change. Ce qui devrait avoir un impact négatif sur les exportations nettes. Mais la banque centrale doit maintenir la parité et offre donc de la monnaie nationale, ce qui accroît la masse monétaire.
Cet accroissement de la masse monétaire accroît l’offre de monnaie sur le marché de la monnaie, ce qui réduit le taux d’intérêt à son niveau mondial. Il n’y a pas d’effet d’éviction du taux d’intérêt sur la demande.
Après le stimulus budgétaire, i reste identique et la masse monétaire a augmenté.
Graphiquement, la modification de l’équilibre se présente ainsi.
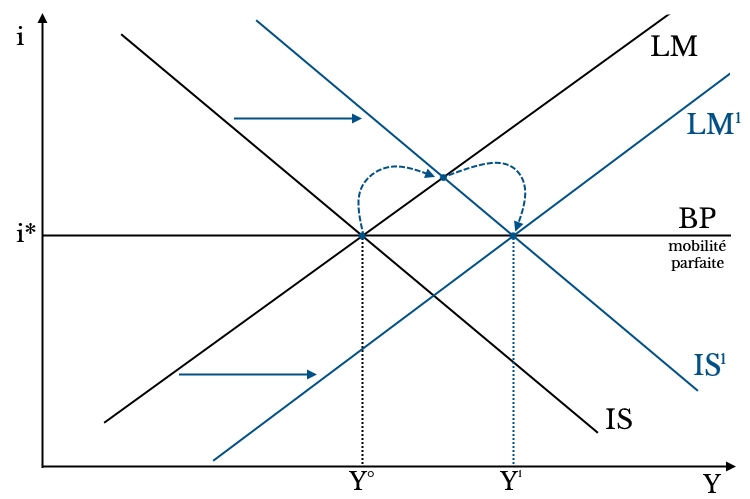
Interprétation du graphique : la hausse de G déplace IS vers la droite. Pour ramener l’équilibre de la balance des paiements (i=i*), LM se déplace à droite. Au final, Y passe de Y0 à Y1.
Politique monétaire en change fixe
Côté politique monétaire, c’est moins joyeux… Imaginons une hausse de la masse monétaire. Le taux d’intérêt diminue pour équilibrer le marché de la monnaie. Cette baisse est supposée avoir un effet positif sur l’investissement et le revenu. En change fixe, la baisse du taux d’intérêt n’est pas compensée par une baisse du taux de change, mais par une intervention de la banque centrale qui réduit la masse monétaire en acceptant d’acheter la monnaie nationale en échange des devises demandées par les investisseurs.
Cette baisse de la masse monétaire ramène le taux d’intérêt et le revenu à leurs niveaux initiaux. Remarque en passant : pourquoi revient-on exactement au même point ? Simplement parce que les mouvements sur le marché des changes ne se stabilisent que lorsque i a rejoint i* et qu’à ce niveau, on retrouve de fait les mêmes valeurs pour toutes les variables, Y compris.
Graphiquement, on a la modification de l’équilibre suivante.
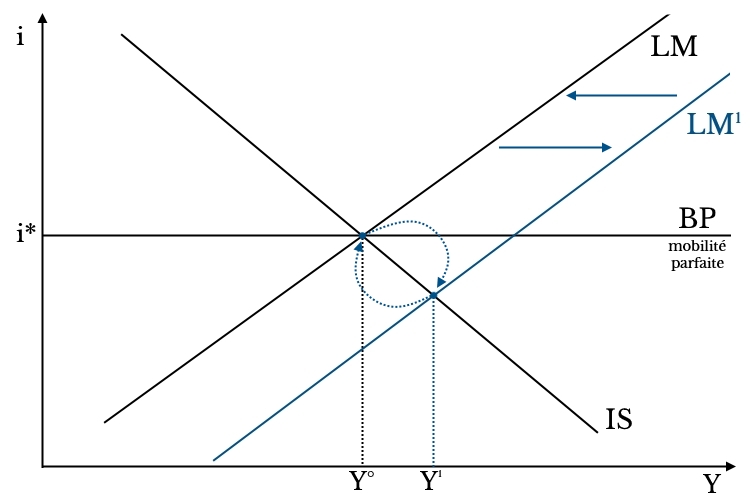
Interprétation du graphique : la hausse de M déplace LM à droite. L’équilibre du moment est Y1. Mais il ne respecte pas l’équilibre de la balance des paiements car i<i*. Les sorties de capitaux réduisent M et ramènent à l’équilibre Y0.
Politiques économiques en change flexible
Principe du change flexible
En change flexible, le marché des changes fonctionne sans intervention systématique de la banque centrale, de sorte que le prix des devises se fixe librement selon l’offre et la demande.
Il faut préciser ici qu’il s’agit de la théorie. En pratique, ce n’est pas le cas (mais ça n’invalide pas l’analyse). Les banques centrales sont des acteurs permanents du marché des changes. Soit qu’elles y réalisent des opérations « techniques » utiles au bon fonctionnement du marché. Soit que, tout en restant dans la philosophie du change flexible, elles ont des objectifs de taux de change plus ou moins marqués. À l’inverse, tous les systèmes de change fixe acceptent des variations réduites du taux de change autour de sa valeur de référence. Au surplus, même dans un système fixe, un pays peut décider de modifier la valeur de référence, par une dévaluation ou une réévaluation de sa monnaie.
Politique budgétaire en change flexible
Le gouvernement augmente les dépenses publiques G. Cette hausse accroît le revenu Y. Cette hausse nécessite une hausse du taux d’intérêt sur le marché de la monnaie pour le rééquilibrer. Cette hausse du taux d’intérêt attire les capitaux. Les entrées de capitaux se traduisent par une appréciation du taux de change. La hausse du taux de change réduit les exportations nettes et donc le revenu. Sur le marché de la monnaie, la baisse du revenu réduit la demande de monnaie, ce qui a pour effet de ramener le taux d’intérêt à sa valeur initiale. Au final, le taux d’intérêt retrouve son niveau initial (le niveau mondial i*, par définition), de même que le revenu Y. Il y a donc un effet d’éviction complet par le biais de la hausse du taux de change.
L’équilibre est modifié ainsi.
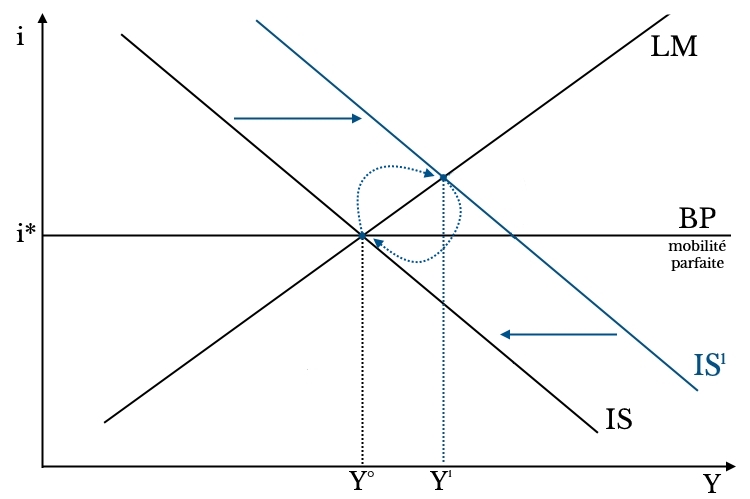
Interprétation du graphique : la hausse de G déplace IS à droite. Mais le nouvel équilibre Y1 est incompatible avec l’équilibre de la balance des paiements car i > i*. Les entrées de capitaux apprécient le taux de change, qui réduit les exportations et ramène IS à sa position initiale en Y0.
Politique monétaire en change flexible
L’offre de monnaie M croît. Cette hausse réduit le taux d’intérêt sur le marché de la monnaie. La baisse du taux d’intérêt accroît l’investissement et Y sur le marché des biens. Sur le marché des changes, elle suscite des sorties de capitaux. Ces sorties ont pour effet de réduire le taux de change. La baisse du taux de change stimule les exportations nettes et donc Y. La hausse de Y accroît le taux d’intérêt sur le marché monétaire, jusqu’à son niveau i* pour rééquilibrer le marché de la monnaie. Ce qui réduit l’investissement. Au total, la hausse de Y est la hausse des exportations nettes, i étant inchangé.
Graphiquement, l’équilibre est modifié de la sorte.
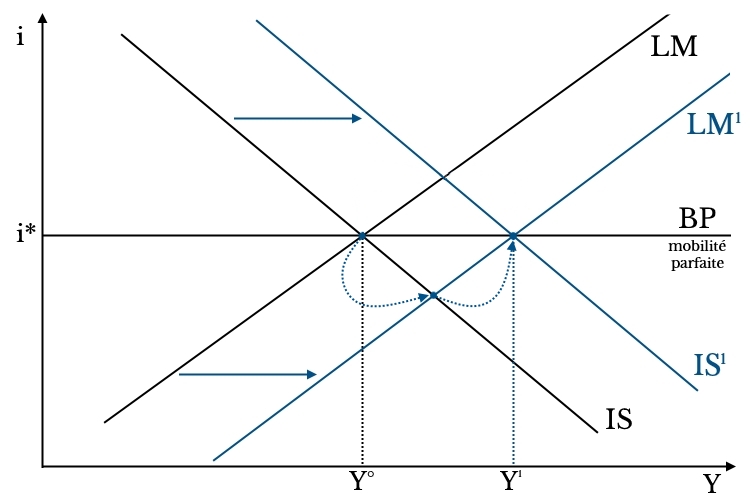
Interprétation du graphique : la hausse de M déplace LM à droite. La balance des paiements est en déséquilibre (i<i*). Les sorties de capitaux déprécient le taux de change. La dépréciation accroît les exportations nettes. IS se déplace à droite. Le nouvel équilibre est Y1. Y est passé Y0 à Y1.
Récapitulatif
On peut dire que dans une petite économie ouverte avec mobilité parfaite des capitaux et prix fixes, on a les choses suivantes.
La politique monétaire en changes flexibles, c’est génial. Cela permet d’accroître les exportations et le revenu. On ne morfle pas à cause de la hausse du taux d’intérêt (qu’on aurait en économie fermée). Et l’ajustement du taux de change permet d’avoir un impact de la hausse monétaire (en change fixe, cette hausse serait contrecarrée par les interventions de la banque centrale pour maintenir la parité).
La politique monétaire en changes fixes, c’est inutile. Ce qui fait l’efficacité de la politique monétaire, c’est la capacité à contrôler la masse monétaire. Or, en changes fixes, les entrées ou sorties de capitaux imposent le niveau de la masse monétaire, pas les décisions de la banque centrale. Et comme toute modification de la masse monétaire produit des mouvements de change qu’il faudra compenser pour maintenir la parité, on ne peut rien faire.
La politique budgétaire est justement efficace en changes fixes. En cas de hausse des dépenses, la pression à la hausse sur le taux d’intérêt induit une pression à la hausse sur le taux de change et contraint la banque centrale à accroître l’offre de monnaie pour maintenir le taux d’intérêt à son niveau initial. Elle évite ainsi l’effet d’éviction du taux d’intérêt sur la demande interne.
Pour finir, la politique budgétaire en changes flexibles est sans effet car en accroissant le taux d’intérêt, elle accroît le taux de change et réduit les exportations nettes du montant de la hausse du revenu attendue.
L’impact des politiques économiques avec quelques équations
Pour compléter l’analyse littéraire et graphique, un peu de statique comparative pour préciser l’effet des politiques économiques.
Impact de la politique économique en change fixe
On différencie IS, LM et BP selon toutes les variables :
dY = AydY + Aidi + AGdG + XNede
dM = LydY + Lidi
di = di*
Fx désigne la dérivée de la fonction F par rapport à x.
Le régime de change fixe implique que de = 0.
Le taux d’intérêt mondial étant donné exogène, di = di* = 0.
Politique budgétaire en change fixe
dG > 0 (ou dT < 0)
Comme A(Y, i, G, T) = C(Y) + I(i) + G – T, on a AG = 1
On a alors :
dY = AydY + dG et dM = LydY
Remarque : comme on a supposé au dessus que XN ne dépend que de e, on peut supposer que les importations sont en fait incluses dans A et leur lien avec Y sera pris en compte dans (les importations croissent avec Y, de sorte que est plus élevée que si seule la consommation est prise en compte.
Finalement :
dY/dG = 1/(1-Ay)
Le multiplicateur du revenu est le même que dans un modèle keynésien sans monnaie. Seul l’effet d’éviction des importations limite la relance. La seconde équation traduit l’accroissement de la masse monétaire consécutive aux entrées de capitaux.
Politique monétaire en change fixe
di = di* = de = dG = dT = 0
dY = AydY + Aidi + AGdG + XNede devient simplement : dY = AydY
Dont on déduit que dY = 0.
Par ailleurs, dM = LydY.
La masse monétaire ne change pas, Y non plus.
Impact de la politique économique en change flottant
On différencie IS, LM et BP selon toutes les variables :
dY = AydY + Aidi + AGdG + XNede
dM = LydY + Lidi
di = di*
Le taux d’intérêt mondial étant donné exogène, di = di* = 0
Politique budgétaire en change flexible
dY = [1/(1 – Ay)](dG + XNede)
dM = LydY = 0
En change flottant, la masse monétaire est exogène, elle ne varie que par la politique monétaire. Il s’en suit que dy = 0 et donc que dG + XNede. La hausse des dépenses publiques est totalement évincée par la baisse des exportations.
Politique monétaire en change flexible
Sur le marché des biens, l’impact de la hausse de l’offre de monnaie se répercute par le biais des exportations dues à la baisse du taux de change :
dY/de = XNe/(1 – Ay)
En définitive :
dY /dM = 1/Ly >0
de/dM = (1 – Ay) / XNeLy <0
