Le premier jeu était trop facile. En voici un plus difficile.
Federer et Nadal sont sur le gazon de Wimbledon. Federer est au service. Il se demande s’il doit servir du côté du coup droit de son adversaire, ou de son côté revers. Nadal se demande s’il doit anticiper un service du côté de son revers ou de son coup droit.
Nadal est meilleur du coup droit que du revers. S’il anticipe correctement un service côté coup droit, il retourne le service de Federer dans 90% des cas. S’il anticipe correctement un service côté revers, il retourne correctement dans 60% des cas.
Si Nadal n’anticipe pas correctement le service, il doit interrompre son mouvement et essayer de récupérer le coup. S’il a anticipé un tir sur son revers et que Federer a tiré vers son coup droit, il renvoie correctement la balle dans 30% des cas; s’il a anticipé un tir sur son coup droit et que Federer a tiré vers son revers, il renvoie correctement la balle dans 20% des cas.
Les deux joueurs connaissent bien les données du problème, issues d’analyses exhaustives de leurs précédents matchs. Comment Federer doit-il servir? Qu’est-ce que Nadal doit anticiper?
EDIT : là encore, bravo à tous les participants qui ont déployé beaucoup de réflexion sur ce jeu. La solution se trouve de la façon suivante :
– Il n’y a pas de solution en stratégie “pure”, c’est à dire qu’il n’existe pas d’action simple pour chacun des joueurs qui soit la meilleure. Federer pourrait se dire qu’il doit tirer vers le revers de son adversaire, plus faible; mais dans ce cas, celui-ci va s’y attendre et anticiper un revers, et dans ce cas Federer doit servir côté coup droit pour réduire la probabilité de balle retournée. De la même façon Nadal ne sait pas comment agir : il peut se dire qu’il vaut mieux anticiper un revers (son moins bon côté) mais il sait que s’il anticipe systématiquement un revers, Federer va tirer sur son coup droit et le prendre ainsi à contrepied.
– La seule solution consiste à chercher à surprendre l’adversaire en adoptant un comportement aléatoire. Mais tous les comportements aléatoires ne se valent pas. Ainsi, si Federer décide, avant chaque coup, de tirer à pile ou face pour décider de son service (il choisit donc un “mix” de stratégies à 50-50) Nadal va lui renvoyer encore beaucoup de balles, il existe une meilleure solution. Pour résoudre le problème, on peut adopter des solutions calculatoires (Gizmo a indiqué celle-ci, Antoine nous a livré des simulations); on peut aussi visualiser cela sur des graphiques. Ainsi :
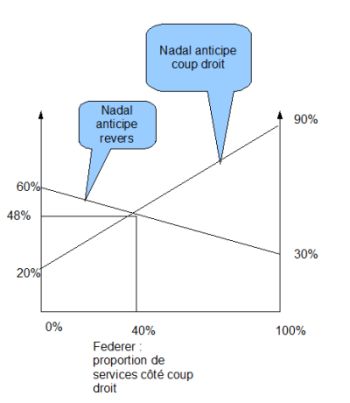
En abscisse, on représente, graduée de 0 à 100%, la proportion de services que Federer tire vers le coup droit de Nadal. En ordonnée, on indique la proportion de retours réussis par Nadal. Puis on indique deux droites de retour : le taux de retour si Nadal anticipe un coup droit, et le taux de retour si Nadal anticipe un revers. On voit alors pourquoi servir par exemple à 50% vers le coup droit n’est pas une bonne solution pour Federer; La meilleure combinaison de services est atteinte à l’intersection entre les deux droites, car c’est le seul point à partir duquel Nadal ne peut pas améliorer son taux de retour en modifiant sa stratégie. Cette intersection est atteinte pour une proportion de 40% de services vers le coup droit. A ce point, le taux de retour est de 48%.
L’application du même raisonnement pour Nadal (chacun peut essayer de faire le graphique) permet de montrer que celui-ci doit anticiper les coups droits à hauteur de 30%; à ce point, son taux de retour est de 48%. Le fait que le taux de retour maximal pour Federer soit égal au taux minimal de Nadal à l’optimum n’est pas surprenant : c’est le théorème de Von Neumann (aka théorème du maximin) qui s’applique (le maximum minimorum de l’un est égal au mnimum maximorum de son adversaire dans un jeu à somme nulle).
Ces calculs ont-ils un sens? Après tout, nous savons que les joueurs de tennis ne s’amusent pas avec une calculatrice et un générateur de nombre au hasard avant chaque coup. On peut penser d’ailleurs que les calculs du genre de ceux qui sont présentés ci-dessus ne sont pas franchement leur tasse de thé. Néanmoins, lorsqu’on applique ce genre de méthode pour voir si le comportement des sportifs correspond à cet optimum théorique, on constate un résultat étonnant : les meilleurs joueurs adoptent un comportement extrêmement proche de la théorie. L’application d’un modèle similaire au football pour les tirs de penalty a ainsi montré que les grands tireurs de penalty et les meilleurs gardiens adoptent, face à chaque adversaire, la meilleure combinaison possible, et ce de façon intuitive.
(Jeu et solutions viennent de thinking strategically, de Dixit et Nalebuff)
- William Nordhaus, Paul Romer, Nobel d’économie 2018 - 19 octobre 2018
- Arsène Wenger - 21 avril 2018
- Sur classe éco - 11 février 2018
- inégalités salariales - 14 janvier 2018
- Salaire minimum - 18 décembre 2017
- Star wars et la stagnation séculaire - 11 décembre 2017
- Bitcoin! 10 000! 11 000! oh je sais plus quoi! - 4 décembre 2017
- Haro - 26 novembre 2017
- Sur classe éco - 20 novembre 2017
- Les études coûtent-elles assez cher? - 30 octobre 2017
J’essaye, c’est a prendre aux erreurs de calcul pres. Nadal doit anticiper a droite avec une probablite de 0,44, et Federer servir a droite avec une probabilite de 0.31.
Il me semble que le couple stratégique (Revers, Revers) soit le meilleur choix pour Nadal et Federer, en effet choisir le revers est, pour Federer, la stratégie lui permettant de s’assurer le plus gros gain (ou minimax) (en l’occurence 40% et 70% de chance que Nadal ne renvoit pas la balle contre 80% et 10%). Nadal, connaissant cette donnée, n’a pas intérêt à dévier du choix du revers, même si, dans un premier temps, anticiper le coup droit serait pour lui plus intéressant, le jeu étant à information complète il doit anticiper le service vers son revers.
Je ne sais pas si on peut parler d’un équilibre de Nash en (revers,revers), je commence juste à apprendre la théorie des jeux (en autoditacte), mais bon c’est en se trompant que l’on apprend !
Merci pour votre site très intéressant.
Les gains pour Nadal sont les pourcentages de bons retours, et les pourcentages de mauvais retours sont les gains de federer (donc la somme des gains est toujours 1).
Il n’y a pas d’équilibre de Nash en stratégies pures (car il y a toujours un intérêt à dévier).
En stratégies mixtes, il me semble que Federer a intérêt à servir côté coup droit dans 40% des cas et que Nadal doit anticiper coup droit dans 30% des cas.
Mais quid des stratégies de montée au filet?
C’est des probas conditionnels je crois, mais après ca se compliqué:
Pour Nadal, proba de renvoyer le balle:
PD/D=0,9
PD/G=0,3
PG/D=0,2
PG/G=0,6
Donc l’anticipation qui marche le mieux, en supposant que Federer envoi autant d’un coté que de l’autre est:
(PD/D + PG/D)/2= 0,55
(PD/G + PG/G)/2= 0,40
Si il choisit d’anticiper aléatoirement à gauche ou a droit, le probabilité de retour du service est:
P=0,475
Mais de son coté, Federer fait le même calcul mais dans le sens inverse et remarque qu’il a plutôt interêt à servir à Gauche:
PG/G + PG/D < PD/D + PD/G
0,4 < 0,55
Nadal se doute bien que Federer a fait se calcul, il va donc modifier son propre calcul en supposant que Federer va servir à gauche à tous les coup, et donc on aura toujours PG/G soit 0,6 alors qu’en servant aussi bien à gauche qu’a droite, il obtient P soit 0,475 que Nadal renvoi le service.
Hors ce résultat n’est pas optimal pour Federer, lui aussi anticipe la réaction de Nadal:
Il doit donc trouver un équilibre, pour pas que Nadal puissent anticiper:
Après je sèche, vois pas comment formaliser l’anticipation de l’un et de l’autre
je m’avancerais sur la stratégie revers
evers
Ils jouent en strategie mixte a l’equilibre (il n’y a pas d’equilibre de Nash en pures strategies).
A l’equilibre, Federer joue cote coup droit avec probabilite 80%, et Nadal anticipe un coup droit avec probabilite 30%.
(Sauf tres possible erreur de calcul.)
Je me suis peut être embrouillé, mais il me semble qu’on ne peut pas répondre par coup droit/revers à aucune des deux questions.
Un petit calcul de probabilité montre que si Federer sert sur son coup droit avec la probabilité p, alors :
* Nadal renvoie le service, en anticipant un coup droit, avec la probabilité 0.2+0.7*p
* Nadal renvoie le service, en anticipant un revers, avec la probabilité 0.6-0.3p
Les deux probabilité sont égales pour p=0.4. En d’autres termes, si Nadal pense que Federer a plus de 40% de chances de servir sur son coup droit, alors il a intérêt à anticiper un coup droit. S’il pense au contraire qu’il y a moins de 40% de chances que le service vient du côté droit il a intérêt à courir vers le revers.
Si on suppose que Federer tire au hasard le côté vers lequel il va servir (ce qui n’est certainement pas le cas !!!) Nadal devrait plutôt courir vers son côté droit.
L’étude symétrique donne la valeur 30 % : si Federer pense que Nadal a plus de 30% de chances d’anticiper sur son coup droit, alors il a intérêt à servir un revers. Sinon, il ferait mieux de servir un coup droit.
Dans les deux cas, il manque un chiffre : avec quelle probabilité Federer sert sur un coup droit ? Ou bien : avec quelle probabilité Nadal anticipe un coup droit ?
Ouf… ça me paraît bien compliqué… j’ai dû me tromper qque part…
Les stratégies sont : pour Federer, "servir à droite" ou "servir à gauche" ; pour Nadal "anticiper à droite" ou "anticiper à gauche". Si on cherche un équilibre en stratégies pures, Federer a toujours intérêt à servir sur le revers, puisque c’est sa stratégie dominante, quelle que soit la stratégie de Nadal. En effet, que Nadal anticipe bien ou non, la probabilité qu’il retourne correctement est inférieure lorsqu’il retourne un revers qu’un coup droit. Donc Federer sert sur le revers de Nadal, et Nadal anticipe un service sur le revers. Si on cherche un équilibre en stratégies mixtes, alors j’y retourne…
Honte sur Gizmo, qui a fait une erreur de raisonnement dans le commentaire précédent. Il ne fallait pas écrire "que Nadal anticipe bien ou non", car les stratégies de Nadal ne sont pas "bien anticiper" ou "mal anticiper", mais bien "anticiper revers" ou "anticiper coup droit". Donc il n’y a pas d’équilibre en stratégies pures. En revanche, si on construit une matrice des gains du serveur, on obtient : (R,R)=0,4 ; (R,D)=0,8 ; (D,R) = 0,7 ; (D,D) = 0,1 où les lettres entre parenthèses représentent les stratégies de (Federer, Nadal), avec R pour revers et D pour coup droit. On pose p la probabilité pour Federer de servir à gauche (et donc (1-p) de servir à droite). On pose q la probabilité pour Nadal d’anticiper à gauche (et donc (1-q) d’anticiper à droite). On maximise conjointement l’espérance de probabilité de réussite de Federer et de Nadal (c’est un jeu à somme nulle : ce que Federer ne gagne pas, c’est Nadal qui le gagne) :
p(q.0,4+0,8(1-q))+(1-p)(0,7q+0,1(1-q)) et q(0.4p+0,7(1-p))+(1-q)(0.8p+0,1(1-q)). On trouve p=0,6 et q=0,7. Donc pour maximiser l’espérance de probabilité de réussite, Federer sert revers 6 fois sur 10 et Nadal anticipe revers 7 fois sur 10. Je sais pas si c’est juste, mais c’est moins faux que précédemment…
Natale doit anticiper un droit dans 30% des cas, Federer doit faire un droit dans 40% des cas.
(preuve sur demande)
Pas d’équilibre de Nash en stratégie pure.
Si mes calculs sont bons, en stratégie mixte, Federer doit servir sur coup droit 40% du temps et Nadal doit anticiper un service sur coup droit 30%.
Si on postule que toutes les informations sont connues des deux joueurs et que chaque joueur sait que l’autre peut anticiper aussi bien que lui, alors,
– Federer doit servir au hasard pur (50/50)
– Nadal sait que Federer servira au hasard s’il est lui-même imprévisible et doit donc anticiper au hasard pondéré par ses pourcentages de réussite : il doit anticiper 60% coup droit et 40% revers.
Ceci étant dit, rien n’est indiqué sur l’aversion au risque des joueurs, et il n’est pas précisé qu’il est beaucoup plus coûteux pour Nadal de rater la balle que pour Federer de voir son service récupéré : dans le premier cas, Federer marque 15 points (ou 10, ou…), dans le second, l’échange continue et on ne sait pas qui va emporter le point. Ca change les calculs. Conclusion : un service au tennis n’est pas un tir au but au foot.
Je dirais que çà dépend essentiellement de comment Federer a servi auparavant.
Sur son tout premier service, il faut sans doute que Federer serve sur le revers (60%) et que Nadal anticipe en revers (60%).
Après, çà se complique…
De toute façon, aujourd’hui, Nadal a mal anticipé !
Mes cours de TDJ sont très loin mais j’ai trouvé:
-Federer doit servir Coup Droit proba 0.4
-Nadal doit anticiper Coup Droit proba 0.3
Soit x la probabilité que Nadal anticipe un service à droite, y la probabilité que Federer serve à droite, G le gain moyen de Nadal en fonction de x et y.
L’équation pour G s’obtient en traduisant l’énoncé:
G=.9xy+.6(1-x)(1-y)+.3(1-x)y+.2x(1-y)
<=> G=.9xy+.6-.6y-.6x+.6xy+.3y-.3xy+.2x-.2xy
<=> G=xy-.4x-.3y+.6
Un graphique 3D de G en fonction de x et y, ainsi que l’examen des min/max de G, permet alors de comprendre que la bonne démarche ne nécessite pas de calculer G…
On peut s’en sortir tout simplement en traçant le graphique du gain de Nadal en fonction du pourcentage anticipé à droite, en distinguant les cas où Federer sert à droite ou à gauche.
Autrement dit traçons deux droites entre les points (0,0.3);(100,0.9) et (0,0.6);(100,0.2). Le bas de ces courbes représente le gain minimal de Nadal en fonction de ce que fera Federer (le haut le gain maximal) . En jouant l’intersection (environ 30% de coup droit), Nadal a bon espoir de retourner au moins 48% des services.
De la même façon, on trace deux droites entre les points (0,0.6);(100,0.2) et (0,0.2);(100,0.9). En jouant l’intersection (environ 35% de service à droite), Federer a une espérance de gain de 45%.
Le 7% restant reviendra à celui qui devinera le mieux les anticipations adverses. Les pentes des courbes indiquent qu’il sera moins risqué à Nadal d’anticiper un peu plus de revers, et moins risqué à Federer de servir un peu plus de coup droit.
Enfin on peut développer l’arbre de probabilité de gain des jeux, et il devient alors évident que Federer gagne en 5 set (calculs laissés à l’étudiant).
A priori, si Federer joue le Cavalier b4 en c6, il fait pression sur le pion e7, et même si cette pression peut facilement être contrée par la présence du fou en b7 au coup suivant (clouant c6 sinon Fxg7 et prend la tour), la colonne ouverte en f (e7-e6 fxe fxe) donnerait à Federer un avantage décisif en fin de partie.
Alekhine et Tartakower ont déjà écrit des articles édifiants sur de telles positions. En jouant les bons coups, Federer fait mat en 24 coups. Enfantin.
Commentaire hors-sujet, mais votre lien vers mon blog sur la barre de gauche pointe vers l’ancienne version…
Jeux très intéressant. Une remarque : je ne suis pas aussi sûr que vous que Federer et Nadal, ou des membres de leurs équipes respectives, n’utilisent pas des méthodes similaires pour développer leurs statégies respectives avant un match. Même chez les juniors (je parle d’expérience), on arrive très vite à des considérations tactiques très élaborées, qui rappellent, même si c’est moins formalisé, la théorie des jeux.
plus cool : je découvre en même temps problème et solution. Ça me
rappelle qu’un magazine de sciences a publié, vers 2001 si mon souvenir est
bon, désolé pour les imprécisions, un dossier complet sur ce sujet des stratégies
des joueurs pour des jeux répétés, avec plein de simulations de plein de
stratégies (dont certaines suggérées par les lecteurs). C’était passionnant. Mais
je crois que l’accent était sur les jeux coopératifs (type dilemme du prisonnier).