C’est ce que l’on pourrait croire en lisant les titres des articles de presse consacrés à une récente méta-étude sur l’efficacité des antidépresseurs type prozac. "Globalement inefficaces", "presque inefficaces", efficacité "sérieusement contestée" nous dit-on. Vraiment? (via Brad de Long)
L’étude citée était une méta-étude, c’est à dire, un travail consistant à synthétiser les résultats de toute une série d’études précédentes. Son résultat peut être représenté sur ce graphique :
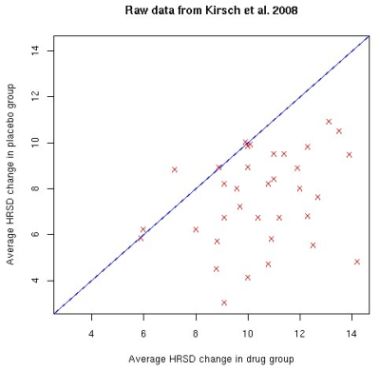
Les axes indiquent l’amélioration moyenne de l’état du malade traité, selon l’échelle d’Hamilton de la dépression. En abscisse, le changement dans le groupe, pour chaque étude, des patients ayant été traités avec un médicament; en ordonnée, ceux qui ont été traités avec un placebo. Un point correspond à une étude, indiquant donc simultanément le score du placebo et celui du médicament. Si un point est sur la diagonale, cela signifie que le placebo a été aussi efficace que le médicament; s’il est au dessus, que le placebo a été plus efficace; s’il est au dessous, que le médicament a été plus efficace.
Vous pouvez juger vous-même : l’écrasante majorité des études a conclu à une efficacité du médicament supérieure à celle du placebo. Ces résultats bruts ont ensuite fait l’objet d’un traitement statistique, qui montre que le médicament apporte en moyenne une amélioration statistiquement significative d’1.8 points. En somme, ce que montre l’étude, c’est exactement l’inverse de ce qui était indiqué dans les titres d’articles : les médicaments, en moyenne, sont plus efficaces qu’un placebo.
Alors d’où vient l’idée qu’ils ne sont pas efficaces? C’est que le National Institute for Clinical Excellence, l’organisme officiel britannique, considère que le critère d’efficacité clinique, c’est trois points de plus qu’un placebo. Or ce critère est assez largement arbitraire, selon les termes mêmes de l’auteur de cette étude. Brad de Long le rappelle très justement : un économiste, face à ces résultats, se poserait la question en termes de coûts d’opportunité. Etant donné que les médicaments apportent une amélioration statistiquement significative de 1.8 points, est-il possible de consacrer les ressources utilisées pour prescrire ce médicament d’une façon qui permettrait d’obtenir un meilleur résultat? S’il existe effectivement des moyens alternatifs permettant d’obtenir un gain de 3, alors le critère a un sens. Sans cela, il ne signifie rien d’autre que la décision arbitraire d’une bureaucratie. Ceux qui ont déduit de cette étude qu’elle "montrait" que les antidépresseurs sont inefficaces devraient réviser quelques notions arithmétiques de base : 1,8 est, aux dernières nouvelles, supérieur à zéro.
Certains placebos sont quand même nettement plus efficaces que d’autres. A se demander pourquoi on n’en prescrit pas plus souvent. Ils sont brevetés ou quoi?
😉
Oui, certains placebos sont plus efficaces: ceux qui sont plus chers!
Voir cet article:sens-commun.blogspot.com/…
"Prenez un médicament. Ou plutôt un placebo, sans aucun effet pharmacologique. Présentez-le à des prix différents. Surprise, il n’aura pas les mêmes incidences sur le mal. Et dans ce cas, le plus onéreux est aussi le plus efficace. Voici la conclusion déroutante à laquelle parvient une étude publiée dans le numéro daté du 5 mars du Journal of American Medical Association."
Réponse de Alexandre Delaigue
Au passage, le bouquin de Dan Ariely (évoqué dans l’article que vous citez) est vraiment très bien.
Merci d’apporter ces précisions !!!
Question : pourquoi AUCUN journaliste n’a-t-il pris la peine de relever ce "détail" ? Et voilà une nouvelle idée reçue lancée dans la population : dans 20 ans on l’entendra encore !
Merci pour cette bouffée d’air frais :-)))
Le graphique est tout-à-fait parlant…
Quant à la "droite de régression", je préfère ne rien dire, pour rester poli ;->
Réponse de Alexandre Delaigue
Pourquoi voudriez-vous tracer une droite de régression sur ce graphique? Il n’y a aucune raison de penser que l’efficacité d’un placebo est corrélée avec celle d’un médicament.
@Oleg: Je pense qu’une des raisons, c’est tout simplement que la notion de "test significatif" est dure a comprendre, meme pour un scientifique; alors pour un journaliste qui n’a pas forcement de formation scientifique… Personellement, je suis utilisateur de statistique dans mes recherches, et j’evite comme la peste les tests statistiques, car ils sont tres difficiles a manier sans faire d’anneries, et je ne suis pas le seul (certains statisticiens preconisent carrement leur abandon, comem J.S Armstrong). Je ne serais pas surpris que parmi les scientifiques qui les utilisent, la majorite en fait n’importe quoi. Un des problemes reside dans le concept de "statistical significance" (qui veut dire que le resultat a peu de chances d’etre du "au hasard"), qui est different du concept de "practical significance". En fait, il y a la comme dans beaucoup de pratiques scientifiques un probleme de vocabulaire.
Bref, il n’est pas etonnant que les journalistes ne le relevent pas lorsque beaucoup de scientifiques eux memes n’en sont pas forcement conscients (ce n’est pas la seul raison non plus).
Un médicament actif (par ex. la Fluoxétine) contient une part d’effet placebo. Dans le gain de 1.8 du médicament il donc de l’effet placebo, d’autant plus que dans le domaine des psychotropes et des troubles psychiques la subjectivité est importante malgré la rigueur de l’échelle retenue (qui contient aussi beaucoup de signes qui peuvent être d’origine somatique, ce qui brouille les diagnostics).
Quant à considérer un gain de 3 et pas 1.8, j’ignore pourquoi.
Parmi les spécialistes les avis sont toujours aussi partagés sur les conclusions de l’étude. C’est soit : "j’avais constaté que ces produits étaient inefficaces pour les dépressions légères ", soit : "l’étude n’est pas du tout concluante, je continue de prescrire". Bref, on n’est pas plus avancés.
Réponse de Alexandre Delaigue
Attention : le gain moyen de 1.8 est le gain EN PLUS de l’effet placebo.
Attention, il s’agit de 1,8 sur une échelle d’efficacité de près de cinquante. En d’autres termes, l’effet est significatif mais proche de zero. Compte tenu des effets secondaires de ce type de médicaments, le ministère de la santé britannique conseille donc de les réserver aux cas les plus lourds, pour lesquels les placebos fonctionnent mal. L’étude est donc pas à côté de la plaque, c’est comme d’hab la presse française qui cherche l’info accrocheuse et qui ne fait aucune remise en perspective!
Réponse de Alexandre Delaigue
Oui, mais on revient au problème : sur quelle base le ministère de la santé britannique décide de son critère?
@ Barca et AD
Merci de l’info, je cours acheter le Dan Ariely en plus du dernier Tim Harford.
Ca me fait penser à certaines discussions en France. Puisque amha l’homéopathie n’est qu’un placebo très élaboré, relativement cher, mais sans doute efficace, il est tout à fait logique (rationnel!) que les médecins la prescrivent. Idem pour les psychothérapies avec le débat en 2003 autour de l’amendement Accoyer (NB : je ne dis pas que les psytp sont des placebos).
D’après Ariely, le coût d’un traitement peut augmenter son efficacité. Freud disait la même chose des psychothérapies (le test en double aveugle en moins). C’est un message très optimiste puisque ça veut dire qu’on doit tendre vers des prix de traitements en rapport avec leur efficacité réelle. En d’autres termes, le marché fonctionne!
Il en va autrement si le coût du traitement est mutualisé, si ses bénéfices sont appréciés par la Haute Autorité de Santé ou le National Institute for Clinical Excellence, et si son remboursement obéit à un logique de budget public.
et puis quel est le seuil de significativité ? 1% ? 5% ? 10 % car ce n’est pas la même interprétation… dans le premier cas on a une chance sur 100 de se tromper contre 10 sur 100 dans le troisième cas… pour un gain de 1,8 la précision est d’importance non ?
C’est comme le R² ou le pseudo-R² dans les régressions : les économistes ont toujours tendance à oublier de préciser sa valeur… or, un faible R² peut remettre en cause pas mal de conclusions du modèle ou en tout cas amène à la plus grande prudence lors des commentaires…
@AAlexandre: c’est pire que ca, une faible p-value ne veut rien dire en soi. Une faible p-value peut tout simplement etre du a un test qui n’est pas puissant: ce n’est pas parce que l’on ne peut pas rejeter H0 que H0 est vraie; aussi, la p-value n’est pas la probabilite que p(H0 | donnees) (c’est pour ca que certains statisticiens deconseillent en general les tests statistiques, pour se rabattre sur les intervalles de confiance, plus facilement maniables, lorsque c’est possible; il existe des cas ou l’on connait les "meilleurs" tests, mais ils sont rares. Le celebre test de Neyman-Pearson est un de cas cas).
@AD: Ma foi je suppose qu’il faut bien fixer un critère, mais ils sont toujours imparfaits. A priori (je ne suis pas médecin) le critère doit prendre en compte le degré d’utilité du médicament versus ses effets pervers (désutilité), ses alternatives (placebo, ou autres traitements) et son coût parce que c’est à la charge de la collectivité. 3 points d’efficacité sur 50 vs placebo, ça ne me semble pas ridicule comme critère même si on ne sait pas d’où il sort exactement.
Maintenant, vu les effets secondaires et que nous sommes les pricipaux croqueurs mondiaux de ces pillules, est-ce que nous ne sommes pas en train de nous créer un problème de santé publique pour rien (ou pas grand chose)? Je ne connais pas L’efficacité réelle des traitements alternatifs, mais causer avec quelqu’un ou s’occuper d’une plante verte, couplé avec un placebo, on doit vite atteindre la même efficacité que les médicaments, non?
Réponse de Alexandre Delaigue
Il y a un critère, qui est celui de la différence statistiquement significative (ce qui est le cas ici). Par ailleurs je vous ferai remarquer que l’échelle d’amélioration totale est entre 4 et 12. Là dessus, un « avantage » de 1.8 ce n’est pas rien. Quant à dire « il faut des critères, mais ils sont toujours imparfaits » ok mais ce n’est pas une raison pour adopter des critères absurdes ou fondés sur rien. Comme indiqué, l’analyse économique fournit un critère, celui du coût d’opportunité : qu’est-ce que cet avantage de 1.8 coûte, et que peut-on faire d’autre avec cette dépense? Sans ce calcul, on est fondé à se demander pourquoi on refuserait à des malades qui souffrent de bénéficier d’un avantage clairement identifié. Si on obtient le même résultat en « causant avec quelqu’un ou s’occupant d’une plante verte » alors oui, c’est probablement moins coûteux (encore que). Encore faudrait-il démontrer que c’est le cas. C’est précisément là que le critère est absurde : Ou sont les coûts et bénéfices des alternatives?
@ David : tiens un économètre par ici ! 🙂
en ce qui concerne les intervalles de confiance en quoi amènent-ils une information plus fine ?
Dans la mesure où on compare avec un placebo et pas avec les traitements alternatifs, il s’agit de savoir si le médicament a le moindre effet réel. Apparemment oui: environ deux points d’amélioration sur cinquante. Dire qu’il fait 1,8 point de mieux que le placebo sur une marge de 4 à 12 points d’effet pour ce dernier Pour le reste, nous sommes d’accord, beaucoup de choses dépendent de la manière dont le critère NICE est conçu: assurer une certaine robustesse au résultat? A priori, il est faible, mais robuste. Se prononcer sur l’utilité du médicament? Là on rentre dans des choses beaucoup plus artisanales. Dans l’idéal il faudrait effectivement comparer les autres possibilités et faire des tests extensifs. Dans quelle mesure ce critère de trois points (ou des 0.5 points de d, j’arrive pas à le comprendre celui-là) est conçu en fonction de ça, dans quelle mesure est-ce qu’il repose sur du pifomètre (c’est à dire des connaissances accumulées)…
Rien à voir, mais comme SM ferme ses commentaires, je vous signale que Krugman a repris ses travaux sur l’impact du commerce sur les salaires. Il semble désormais penser que les choses sont moins évidentes qu’il y’a 10-15 ans:
http://www.princeton.edu/~pkrugm...
@AAlexandre: je ne suis pas du tout econometre, je ne connais rien a l’economie 🙂 Les intervalles de confiance ne sont pas plus fins, ils sont juste plus maniable dans les conclusions qu’ils amenent; l’argument des statisticiens, c’est de ne faire des tests statistiques que lorsque les hypotheses sont bien definies, et de preferer les intervalles de confiance en general lorsque c’est possible (notons que ceux-ci aussi ne sont pas si faciles a manier, de nouveau parce que certains parametres ne sont pas interpretables comme probabilite, mais le sont quand meme).
Le coeur du probleme ici, c’est la difference entre statistiquement significatif et "reellement" significatif. On fait tres regulierement le saut de l’un a l’autre, alors que ce n’est pas justifie (ce que dit AD, c’est qu’une analyse cout-benefice pourrait justement donner un cadre d’analyse pour passer de l’un a l’autre dans ce cas precis). Ces outils sont tres subtiles a manier, et c’est dommage que beaucoup de scientifiques ne prennent pas le temps de bien les comprendre.
@ David : tiens un statisticien par ici alors 🙂
Ok merci pour les réponses… c’est clair que le saut entre "statistiquement significatif" et "réellement significatif" est plus que fréquent chez les économistes… pourtant c’est pas faute d’avoir été prévenu dans les cours de stat et d’économétrie : il ne s’agit que de maniement de chiffres, rien d’autre… d’ailleurs, il suffit de coder ses variables autrement, d’élargir ou de restreindre l’ampleur des classes etc… pour jouer sur la significativité des résultats…
@Alexandre Delaigue
"Pourquoi voudriez-vous tracer une droite de régression sur ce graphique? "
Parce que l’effet placebo, commun à la pillule placebo et la pillule médicament, varie d’études en études. L’infirmière était-elle jolie? L’emballage des pillules de couleur rouge? Cela et milles petits facteurs peuvent jouer et sont spécifiques à chaque étude. Donc tracer une droite de régression passant par l’origine ne semble pas illégitime.
Enlevez 1, multipliez par 100, et ça donnera le pourcentage d’effet lié au médicament. Habituellement en dessus de 30% l’effet est significatif. C’est une règle sur le pouce pas tellement mieux fondé que le +3 cité, mais je trouve rigolo de voir que, à vue de nez, la droite montrerait 50%. Amusant n’est-ce pas? 😉