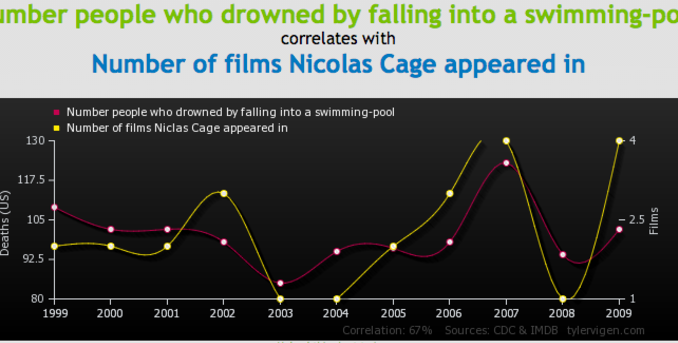
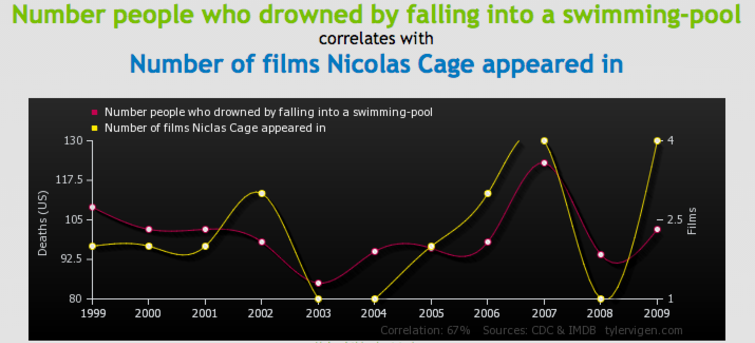
Il est paru il y a deux semaines, sur Vox. Je vous livre le lien sans commentaires. Ça parle tout seul de la différence entre corrélation et causalité (maintes fois abordée sur ce blog).
J’ai choisi pour illustrer le billet ma corrélation préférée. Hélas, c’est aussi celle dont le r est le plus faible. Mais c’est pas grave…
C’est là que je suis triste de ne plus faire mon cours de statistiques descriptives 😉
Et ce qui m’a rappelé de vous parler de l’article, c’est cet article qui montre bien que, parfois, corrélation EST causalité (et que je peux faire preuve de beaucoup de mauvaise fois quand je m’y mets).
- Sur le passeport vaccinal - 18 mai 2021
- Laissez le temps de travail en paix - 19 mai 2020
- Élinor Ostrom, le Covid-19 et le déconfinement - 16 mai 2020
- Ne tuons pas l’enseignement à distance. Optimisons-le - 15 mai 2020
- Quelques commentaires sur les évaluations à l’arrache des systèmes de santé en pleine épidémie - 9 mai 2020
- Du bon usage du supposé dilemme santé vs économie - 9 mai 2020
- Le problème avec la courbe. Édition Covid-19 - 4 mai 2020
- Reprise d’activité - 21 avril 2020
- Problème corrigé sur les notes de lecture - 6 février 2020
- éconoclaste a 20 ans. Épisode 2. Passeurs dans les années 2000 - 27 décembre 2019
Non, non, non, non!
J’ai l’impression qu’à chaque qu’on entend “corrélation n’implique pas causalité”, les gens confondent corrélation, corrélation fallacieuse, significativité statistique et interprétation causale.
On peut avoir une authentique corrélation qui ne correspond pas à une causalité, c’est une chose (parce qu’on a une causalité inverse, ou une variable qui cause deux autres).
Mais dans tous les exemples de Vox, ce n’est pas le problème. Il s’agit plutôt de cas où il y a une corrélation empirique non nulle, mais qui n’a aucun sens théorique. C’est dû à trois raisons:
1) Pas assez d’observations: les écarts-types des estimateurs doivent être très mauvais vu qu’on a qu’une dizaine d’observations, donc pas sûr qu’ils soient significatifs (en pratique, difficile à évaluer vu que n est même trop petit pour appliquer le TCL)
2) Même si la corrélation est significative, cela peut être un coup de chance. On a tellement de données de nos jours, que même une corrélation qui n’a qu’une chance sur mille d’être due au hasard finira par arriver par hasard.
3) Le principal problème: presque tous ces exemples sont des cas de séries temporelles intégrées (OK, c’est discutable pour l’exemple de l’article, ce qui explique peut-être qu’il s’agit d’une des plus mauvaises corrélation, mais c’est le cas de presque tous les exemples de Vox). Or on sait que le coefficient de corrélation entre deux séries temporelles intégrées même complètement indépendantes ne tends pas vers 0. Donc on peut s’amuser à régresser ce genre de séries l’une sur l’autre, mais ça n’a aucun sens!
C’est peut-être du pinaillage de statisticien, mais c’est important de distinguer l’absence de significativité statistique (dans quel cas on ne peut rien dire du tout) et la corrélation sans effet causal (qui permet au moins de faire des prévisions, à défaut de permettre des recommendations de politiques). C’est encore plus important de faire savoir qu’on est capable de distinguer ces deux cas, ça nécessite juste un peu de travail. Autrement, on ne fait que nourrir une espèce de nihilisme concernant les statistiques auprès du grand public.
Je suis tout à fait d’accord.
Ce sujet appelle évidemment à un lien vers la meilleure blague de tous les temps (enfin, si vous êtes dans ce genre de trucs):
http://xkcd.com/552/
Je pense que tout dépend de la méthode employée pour chercher des variables corrélées en 1er lieu.
Un grand classique : le taux de suicide (ou tentatives) des adolescents, selon qu’ils soient homosexuels. Intuitivement, il va être beaucoup plus élevé. Et il l’est. Mais avant même de regarder les statistiques, on peut intuiter plusieurs explications théoriques. En fait ici, la difficulté est de trancher entre elles.
Mais pour un nombre suffisant d’échantillons, il y a une probabilité très faible d’obtenir une corrélation PAR HASARD alors que vous aviez choisi ces variables avec déjà une explication théorique en tête.
Par contre, si vous injectez toutes les statistiques recueillies dans votre logiciel de calcul (par curiosité, lequel vous utilisez ?) et lui demandez d’en trouver des qui soient corrélées, il y en a forcément des qui sont corrélées par hasard. Chercher des explications théoriques à des corrélations trouvées ainsi est très malsain.
Au fait, Stéphane ou Alexandre, vous avez lu la théorie de Maurice Allais sur la distance des lunes aux planètes ? C’est le seul homme capable de faire une régression en démontrant qu’il a proportionnalité entre deux courbes AVEC UN SEUL POINT !
Une théorie sans statistiques ne vaut rien. Des statistiques sans théorie attendent une théorie.