La mesure des inégalités pour les nuls (et les autres)

Je ne vous apprends rien si je vous dis qu’il existe « quelques » débats sur les inégalités. Tous, enfin tous ceux qui sont un peu sérieux, démarrent avec des indicateurs d’inégalités et, généralement, avec des comparaisons dans le temps ou l’espace. Spontanément, je n’aurais pas eu l’idée de pondre un billet sur ces indicateurs, les supposant assez bien connus de beaucoup de gens (et, facilement accessibles, par ailleurs). Mais, comme il y a quelques mois, quelqu’un qui découvrait le blog m’a signalé que « pour les nuls » était passablement exagéré et que, non, ceux qui n’y comprennent rien, ne comprenaient rien à ce que j’écrivais, j’ai réfléchi. Et voilà ce que j’espère être un billet pour les nuls (et les autres).

Je vais retenir quelques indicateurs qui sont le plus fréquemment utilisés pour mesurer les inégalités de revenus ou de patrimoine, notamment dans la presse. Vous verrez qu’on peut aussi s’amuser à appliquer un de ces outils à des choses plus légères. Le premier indicateur est « la part du revenu total détenue  par les x%» (ou la même chose avec le patrimoine). Le second est le « rapport interdécile D9/D1 ». Le dernier est « l’indice ou coefficient de Gini », qui est construit à partir d’un indicateur visuel, appelé « courbe de Lorenz ». Chaque indicateur parle plus ou moins de lui-même, quand on a donné sa définition. Je ferai néanmoins un commentaire final pour montrer que tout seul, assez trivialement, il n’en dit pas plus que ce qu’on peut en attendre. Et qu’il est bon de les observer en même temps. Dans ce qui suit, je ferai référence aux inégalités de revenus. Mais ça fonctionne aussi bien avec n’importe quel autre critère.

Par ailleurs, comme ce texte ne s’adresse pas aux initiés, je vais éviter au maximum le jargon des statistiques descriptives (fréquences, fréquences cumulées, etc.).

La distribution des revenus

Les trois indicateurs reposent sur la construction de la distribution des revenus dans une population donnée. On va relever les revenus des individus, les classer ensuite par ordre décroissant. Et découper la population en tranches, exprimées en pourcentages de la population. On pourra alors dire des choses comme « 20% de la population gagne entre 10 et 20 » ou « 90% de la population gagne moins que 25 » ou encore « 40% de la population gagne au moins 15 ».

Exemple. On a relevé les revenus d’une population constituée de 20 individus. Ce qui donne, en vrac, ceci :
On classe par ordre décroissant de revenu :

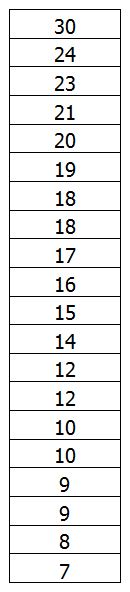
On découpe ensuite la population en tranches de x%. Je vais prendre 10% ici (on parle de « déciles »). Mais on pourrait prendre n’importe quel degré de finesse dans le découpage (1% par exemple ou « centiles »). Quand on regroupe les individus par tranches de 10% de la population, on a, dans ce cas précis, des groupes de 2 individus (20/10) :

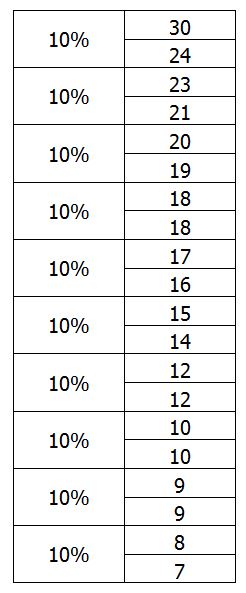
On repère donc déjà que « les 10% les plus pauvres gagnent au maximum 8 » ou que les 10% les plus riches gagnent au minimum 24 ». On va cumuler les groupes afin de pouvoir en dire un peu plus :

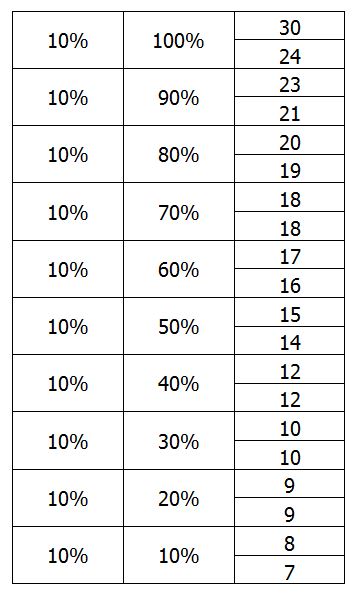
On peut dire, par exemple, que « les 20% les moins riches gagnent au maximum 9 » ou que « 80% gagnent moins de 19 ». Par déduction, il est également possible de dire que si les 20% les moins riches gagnent au maximum 9, alors « 80% gagnent plus de 9 ». C’est déjà intéressant. Mais pour évaluer les inégalités, on va chercher d’autres indicateurs.

La part du revenu détenue par les x%

En prenant le découpage en déciles et en tenant compte des revenus de chaque groupe, on peut facilement donner un premier indicateur, la part du revenu total détenue par les 10% les plus riches.  Dans un monde totalement égalitaire, chaque individu disposerait de la même part du revenu que les autres. Dans un groupe de 10 individus, chacun aurait alors 1/10 du revenu, soit 10%. Donc, toujours dans ce monde, un groupe de 10% des individus détiendrait 10% des revenus. Si le pourcentage détenu par un groupe de 10% dépasse 10%, c’est qu’il existe des inégalités. En calculant la part du revenu détenue par les 10% les plus riches, on a donc une première idée du niveau d’inégalités.

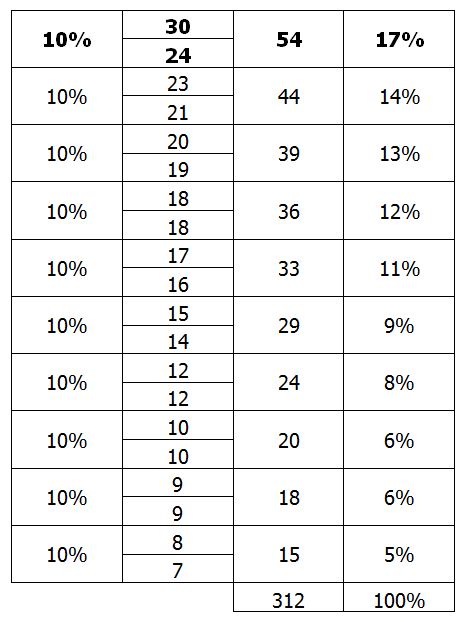
Les 10% les plus riches ont ensemble un revenu cumulé de 54 (30+24). Le revenu total est lui de 312. La part dont dispose les 10% les plus riches dans le revenu total est donc de 17%. Par conséquent, les 90% se partagent 83% du revenu. Ce qui est une situation d’inégalité modérée.

À titre d’exemple, voici l’évolution au cours du 20^ième siècle de la part des 10% ayant les plus hauts revenus dans le revenu total pour un certain nombre de pays.

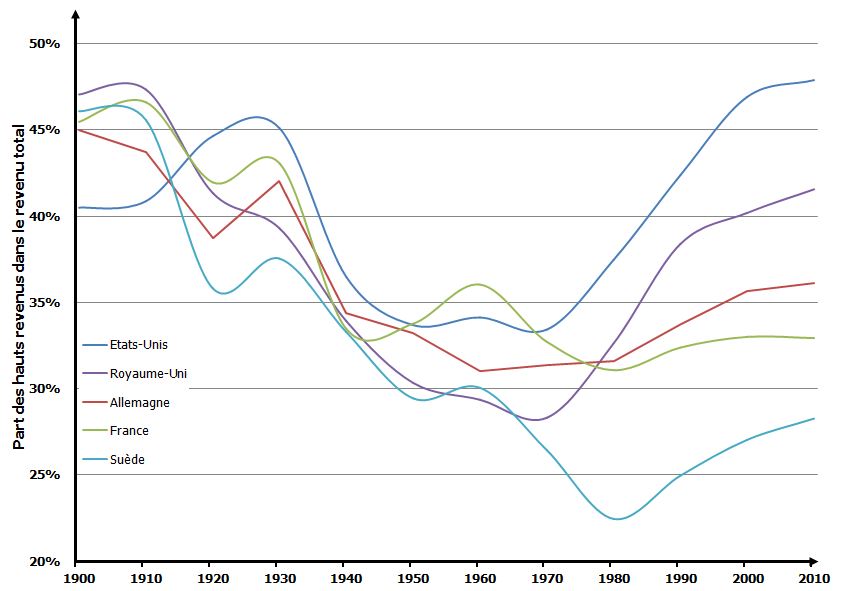
Source : Piketty, « Le capital au 21^ième siècle », Seuil, 2014. Données disponibles ici.

À partir de ce indicateur, on peut dire que le partage du revenu national a eu tendance à évoluer défavorablement pour les 10% jusqu’aux années 1970. Depuis, leur position s’est améliorée, ce qui traduirait une hausse des inégalités. Mais seulement quand on compare la situation des 10% au reste de la population. Cela ne nous dit rien de ce qui se passe en dessous, où les inégalités peuvent se réduire à l’intérieur des 90%.

Le rapport interdécile D9/D1

Le rapport interdécile exploite les données de la distribution de revenus pour évaluer, sous forme de ratio, l’écart entre le revenu limite nécessaire pour faire partie des 10% les plus riches et le revenu nécessaire pour être le mieux loti des 10% les plus pauvres. Si ce rapport est de 5, cela signifie que n’importe quel riche gagne au moins 5 fois plus que n’importe quel pauvre et que ce qui sépare la catégorie des riches de celle des pauvres est un écart de revenu d’un facteur 5.

Un décile est un niveau de revenu maximum rattaché à un groupe représentant x% de la population. Dans un tableau précédent, on a représenté les déciles sans le préciser explicitement. On note les déciles D1, D2, D3, etc.

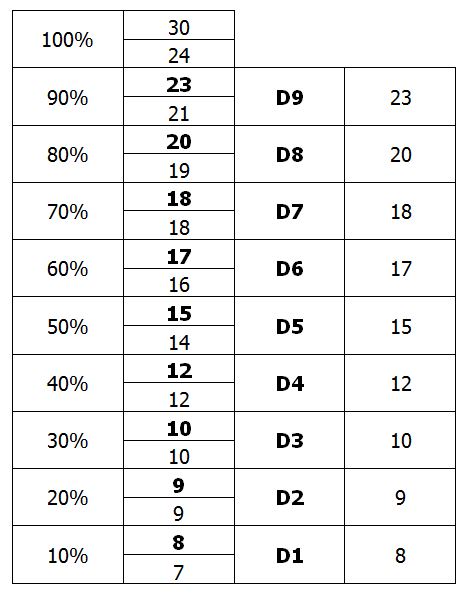
Ici, le rapport D9/D1 vaut donc 23/8, ce qui fait 2,875. On l’interprétera en disant que le revenu des plus riches est environ 3 fois supérieur à celui des plus pauvres.

Le rapport interdécile est un indicateur qui mesure une « polarisation ». Il s’intéresse aux extrêmes de la distribution des revenus, sans se préoccuper de ce qui se passe au milieu. Il est possible de calculer d’autres rapports interdéciles (D8/D2, par exemple), selon la définition des pôles qu’on veut retenir. Plus il est élevé, plus les inégalités le sont.

À titre d’exemple, voici l’évolution du rapport D9/D1 pour les salaires (et pas l’ensemble des revenus) dans quelques pays de l’OCDE.

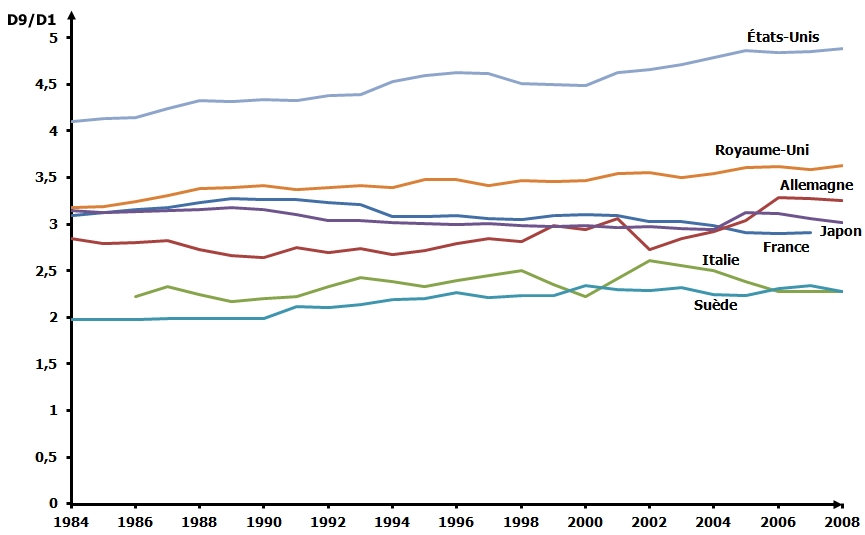
Source : OCDE.

Globalement, depuis les années 1980, le rapport interdéciles des salaires est resté relativement stable dans certains pays (dont la France), mais a significativement crû dans quelques-uns.  Ce résultat peut étonner, par rapport à l’intuition d’une polarisation croissante des rémunérations.  Cela est attribuable au découpage choisi. Retenir un seuil de 10% pour les plus riches (D9) repose sur l’idée que le dernier décile est parfaitement homogène. Or, l’évolution des salaires des 5% les plus riches ou des 1% les plus riches n’a rien à voir avec celle de ceux qui se situent juste en dessous d’eux dans la distribution des revenus. Dans notre petit exemple numérique, par exemple, on note que pour passer des 10% les plus riches aux 5%, il y a un écart de revenus de 6 (30-24), qui est assez important, compte tenu de l’échelle des revenus. Les 5% (l’individu aux plus hauts revenus, avec 30) gagnent 25% de plus que le plus pauvre des 10% (qui gagne 24).

Le coefficient de Gini

Contrairement aux deux indicateurs précédents, le coefficient de Gini est une mesure globale des inégalités, sur toute la distribution des revenus. Tous les écarts de revenus à l’intérieur de la population sont pris en compte, pas seulement ceux qui concernent la comparaison entre les plus riches et les plus pauvres. C’est une grandeur numérique obtenue à partir d’un raisonnement graphique, connu sous le nom de « courbe de Lorenz ». La courbe de Lorenz établit tout au long de la distribution des revenus la part du revenu qui revient aux x% les moins riches. Grâce à elle, on visualise alors quelle part des revenus détiennent les 1% les moins riches, les 2%, etc. Jusqu’à arriver à 100% de la population.

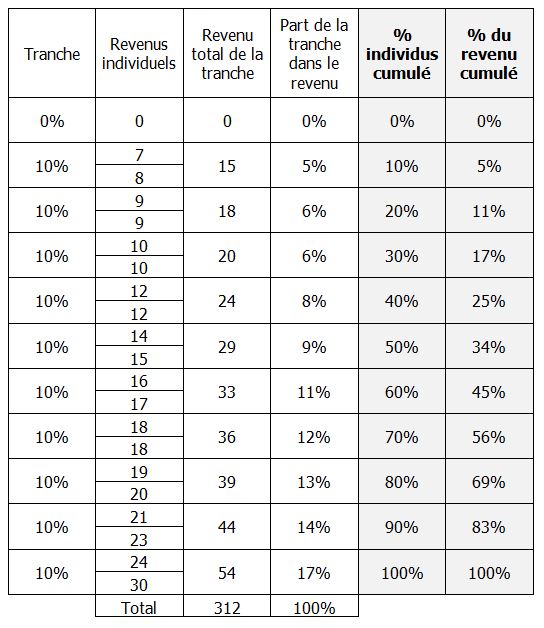
Ce sont les deux dernières colonnes qui nous intéressent ici. La première ligne est évidente : 0% des individus disposent de 0% du revenu total. La dernière, tout autant : 100% des individus disposent de 100% du revenu total. On peut lire la 4^ième ligne, par exemple, de la façon suivante : « 30% des individus disposent de 17% du revenu total ». On trace ensuite la fameuse courbe, en mettant en abscisses le % d’individus cumulés et en ordonnées le % du revenu total dont ils disposent.

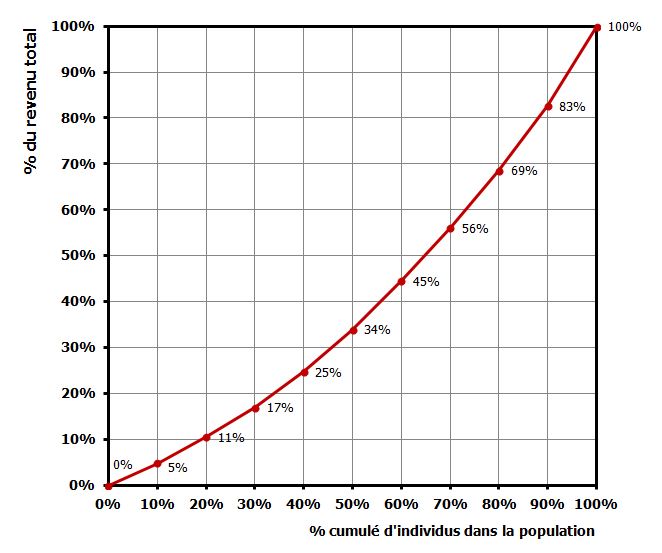
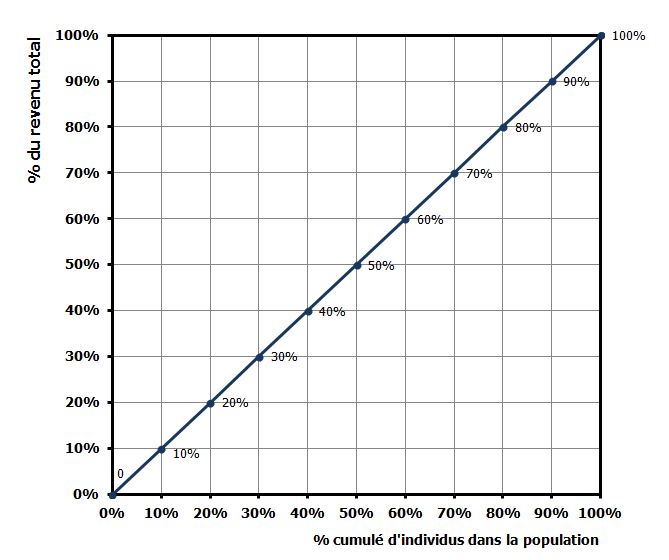
À ce stade, c’est bien mignon, mais ça ne nous dit pas grand chose de plus que le tableau dont elle est déduite. Pour donner un sens en termes d’inégalités, il faut remarquer à nouveau qu’une distribution égalitaire est telle que 1% dispose de 1% des revenus, 2% de 2%, etc. Cette courbe de Lorenz particulière se représente facilement, c’est la droite d’équation y = x ou bissectrice. Dès lors, toute courbe qui s’éloigne de cette bissectrice traduit un certain degré d’inégalités.

La situation la plus inégalitaire est celle où un seul individu dispose de la totalité des revenus. La courbe de Lorenz a cette tête là, si on garde les données de notre petit exemple.

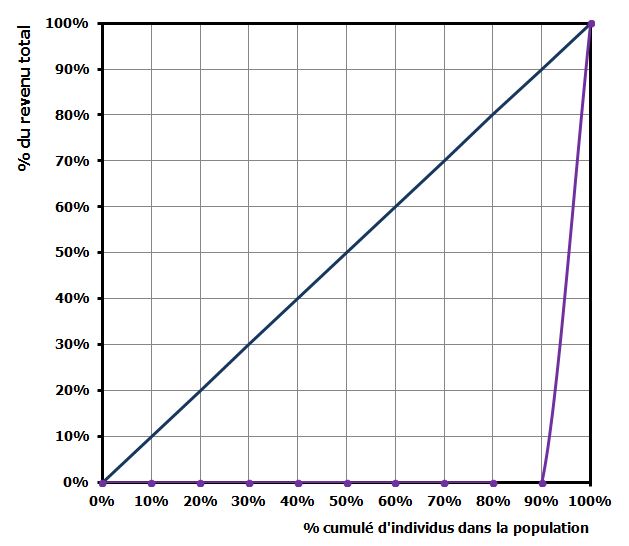
Notez au passage que cette courbe devrait être quasiment confondue avec le triangle ABC de la figure suivante. Des histoires de maths, de taille d’échantillon et autres histoires de limites, qui ne vous intéressent pas trop, je pense, font que graphiquement, ce n’est pas le cas. Mais gardez à l’esprit que la courbe vraiment la plus inégalitaire est représentée par les droites AB et BC (ce sera important pour plus tard).

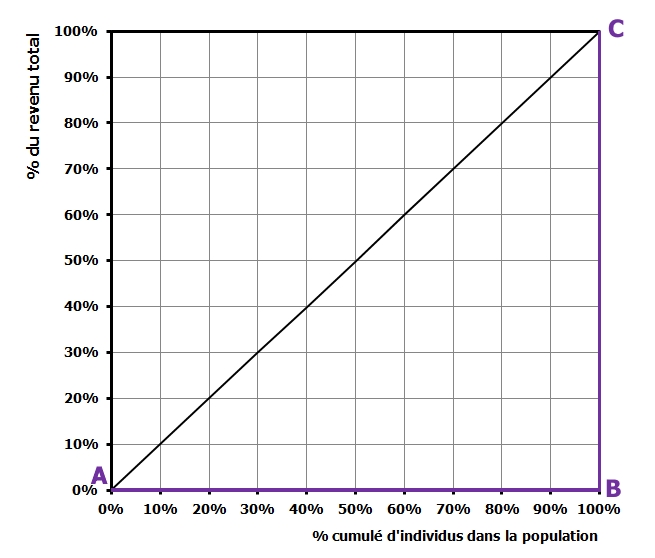
La plus égalitaire des distributions est celle représentée par la bissectrice. Plus on se rapproche de la courbe extrêmement inégalitaire et plus il y a d’inégalités. Mais que signifie « se rapprocher » ? Dans l’exemple suivant, on voit bien que la courbe bleue est toujours plus loin de la bissectrice que la courbe verte. La courbe bleue présente donc une distribution plus inégalitaire que la courbe verte.
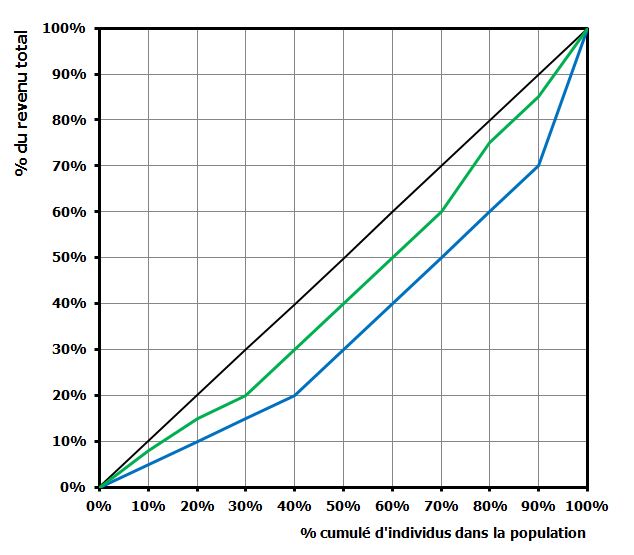Maintenant, dans le cas suivant, comment déterminer laquelle des deux distributions est la plus inégalitaire ?
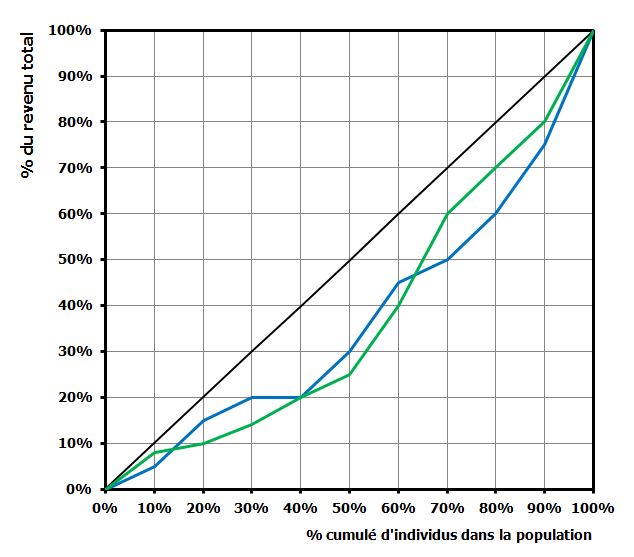Pas évident. Sur certaines portions des distributions, c’est la « population bleue » qui connaît plus d’inégalités, alors que c’est l’inverse sur d’autres portions. En fait, le seul moyen de le savoir est de mesurer la surface entre la bissectrice et chacune des courbes. C’est cette surface qui prendra en compte l’ensemble des inégalités sur la totalité de la distribution.
Le calcul de cette surface, que l’on appelle « aire de concentration », à partir des données de la distribution, est techniquement assez simple, mais fastidieux. Je vous épargnerai donc les détails. Arrivé à ce point, on a presque fini. En fait, on pourrait déjà comparer les différentes distributions et dire laquelle est la plus inégalitaire. Mais obtenir le coefficient de Gini demande une étape de plus.

Le coefficient de Gini est un ratio qui compare l’aire de concentration de la courbe étudiée à l’aire de concentration maximale possible, à savoir celle de la distribution extrêmement inégalitaire. Celle-ci est l’aire du triangle ABC du diagramme précédent. Par construction, elle est égale à ABxBC /2 (surface d’un triangle rectangle). Or, AB et BC ont une longueur de 1. Donc, l’aire maximale de concentration est ½ et le coefficient de Gini (noté G) se calcule en faisant Aire de concentration de la distribution divisée par ½. Ce qui revient à : G = Aire de concentration x 2

Évidemment, plus le coefficient de Gini est élevé, plus les inégalités sont marquées. Par ailleurs, l’indice de Gini est toujours compris entre 0 et 1. La valeur zéro correspond à une distribution égalitaire avec une aire de concentration nulle (c’est la courbe de Lorenz bissectrice). Celle de un correspond à la distribution extrêmement inégalitaire, pour laquelle l’aire de concentration vaut ½ (et donc G = 1).

À titre d’exemple, voici les coefficients de Gini (après redistribution) dans certains pays de l’OCDE (ou associés), en 2012.
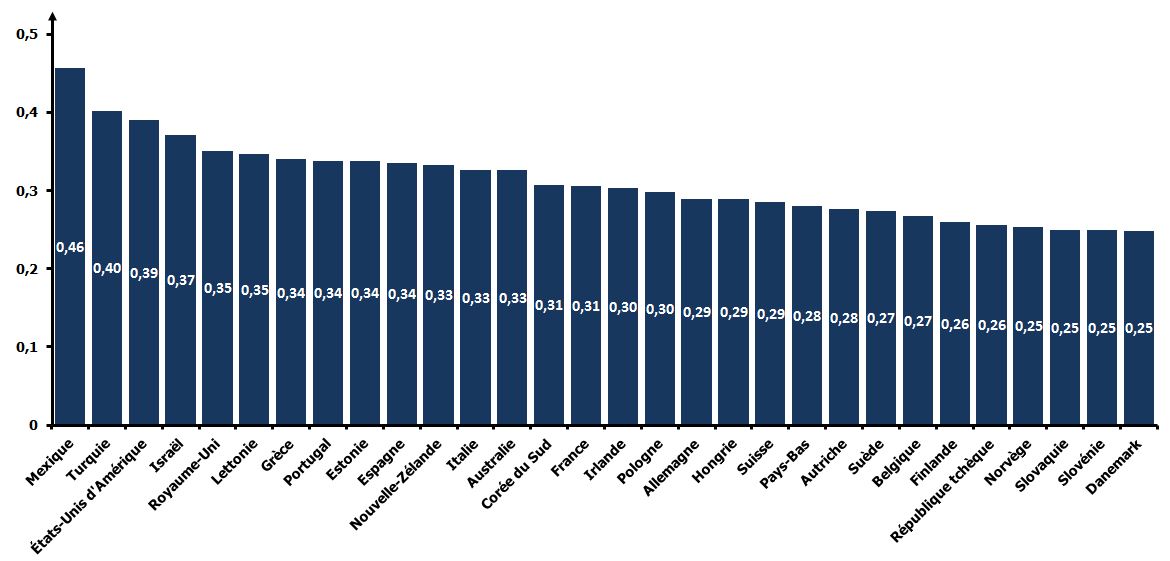Source : OCDE

Notez que, parfois, les coefficients de Gini sont donnés sous forme d’indice, en multipliant par 100 la valeur du coefficient. L’indice est alors compris entre 0 et 100. Ce qui ne change rien à son interprétation.

Pour se détendre un peu, voici les courbes de concentration des buts pour le PSG et l’OM durant la saison 2015-2016. Deux courbes qui sont assez similaires. C’est probablement là que la comparaison s’arrête entre les deux équipes.

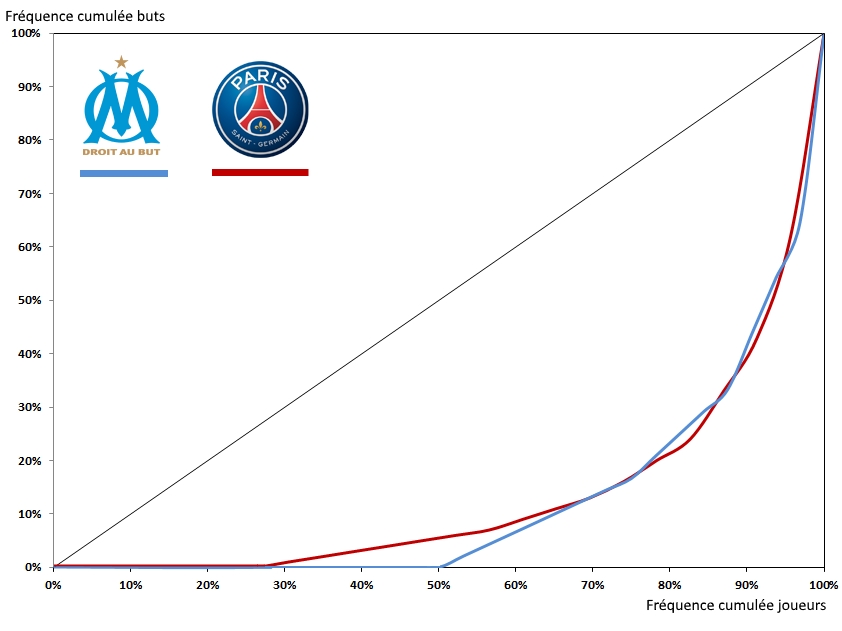
Source : LFP

La grande concentration dans les deux cas n’est pas une surprise. La plupart des équipes présente une courbe de Lorenz fortement inégalitaire. Pour une raison simple : dans une équipe de football, il y a des gens qui sont employés pour marquer des buts et d’autres pour empêcher que cela n’arrive. D’autres, enfin, pour faire un peu les deux. Il est donc normal que les buts marqués le soient par un petit nombre de joueurs. Néanmoins, le haut de la courbe est toujours intéressant. Si elle montre très brutalement, c’est que l’équipe est extrêmement dépendante à un tout petit nombre de buteurs (c’est le cas pour le PSG avec Ibrahimovic et pour l’OM avec Batshuayi). Si la courbe est assez peu inégalitaire, cela signifie que de nombreux joueurs marquent. Cela peut être lié à un style de jeu (où tout le monde attaque et défend), à un grand nombre de buts sur coups de pied arrêtés (où les défenseurs peuvent s’illustrer) ou simplement à des carences chez les attaquants, laissant un pourcentage de buts importants aux joueurs des autres postes.

Quelques remarques de conclusion

Hormis le cheminement dans la construction du coefficient de Gini, les indicateurs d’inégalité communément utilisés ne posent pas de gros problèmes de compréhension. Mais aucun ne donne une vision définitive des inégalités. On l’a vu avec le ratio D9/D1, dont le choix systématique peut être une erreur quand les inégalités sont encore plus élevées à l’intérieur du décile supérieur qu’avec le reste de la distribution. On peut éventuellement corriger un peu ce biais en utilisant non plus les déciles, mais la moyenne ou, mieux, la médiane des revenus des 10 % du haut et du bas. Mais là encore, ce n’est pas parfait.
De même, une part du revenu relativement modeste pour le décile supérieur peut très bien masquer des inégalités très fortes entre classes moyennes et ménages les plus modestes.
À l’inverse, le coefficient de Gini analyse les inégalités en prenant en compte tous les étages de la distribution, mais ne peut pas nous informer sur une possible polarisation aux extrêmes, un phénomène qui mérite pourtant qu’on s’y intéresse. La conclusion de tout cela est assez simple. Il faut se référer à plusieurs indicateurs, dont chacun apporte une partie de l’information utile.

Et maintenant, vous pouvez enfin lire tous les tableaux et graphes fournis par Thomas Piketty dans son bouquin…
La banque mondiale communique également ces données utiles sur le sujet.
En France, l’observatoire des inégalités est une source de synthèse de grande qualité.
Et pour finir, je vous signale, si vous ne le connaissez pas, le blog de Branko Milanovic, l’un des plus éminents spécialistes actuels des inégalités.