Trois liens pour jouer au plus beau des modèles.
Un lien direct vers un applet java.
Une page où l’on peut télécharger un programme simulant le modèle de Schelling.
Une autre page à applet.
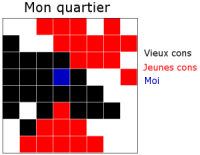
Bonne ségrégation.
- Sur le passeport vaccinal - 18 mai 2021
- Laissez le temps de travail en paix - 19 mai 2020
- Élinor Ostrom, le Covid-19 et le déconfinement - 16 mai 2020
- Ne tuons pas l’enseignement à distance. Optimisons-le - 15 mai 2020
- Quelques commentaires sur les évaluations à l’arrache des systèmes de santé en pleine épidémie - 9 mai 2020
- Du bon usage du supposé dilemme santé vs économie - 9 mai 2020
- Le problème avec la courbe. Édition Covid-19 - 4 mai 2020
- Reprise d’activité - 21 avril 2020
- Problème corrigé sur les notes de lecture - 6 février 2020
- éconoclaste a 20 ans. Épisode 2. Passeurs dans les années 2000 - 27 décembre 2019
bonjour
ne peut on considérer que le modèle présenté relève de la catégorie plus large des "automates cellulaires" utilisés en physique ( par exemple pour simuler la propagation d’un feu de forêt )
Réponse de Stéphane Ménia
Je ne connais pas grand chose à cela, mais il y a certainement une parenté. A quel degré ? Je veux dire, à quelle classe plus générale appartiennent tous ces modèles ? Est-il finalement pertinent de les comparer (après tout, ce sont tous des modèles dynamiques, ce qui est une classe pour le moins large…) ? Le propre du modèle de Schelling, c’est une dynamique assez “complexe”, basée sur des comportements très simples. Dans le livre de Tim Harford que je lis en ce moment, un article récent qui est cité utilise des spécifications plus complexes et réalise des simulations dans l’esprit de Schelling pour montrer l’évolution possible du niveau de corruption dans une société. Ca peut vous intéresser. C’est consultable ici.
Est-ce que ce genre de papiers ne rentre pas également dans la même catégorie ?
http://www.geoffrey-hodgson.info...
J’ai plusieurs fois assisté à des conférences de l’un des deux auteurs et discuté avec lui. Selon lui, ce genre de modélisation est appelée à se développer de plus en plus… même si pour l’instant elle a du mal à passer dans les plus grandes revues apparemment.
Réponse de Stéphane Ménia
Oui, à vue de nez, c’est du genre. De la simulation sur l’apprentissage. De façon générale, ça fait 10 ans que les modèles avec simulations sont jugés potentiellement intéressants pour traiter certaines questions qui se prêtent mal à une démonstration théorique avec équilibre unique et qui sont non expérimentables ou testables en grandeur nature. L’intérêt, me semble-t-il, c’est de montrer qu’avec un modèle donné, réputé sérieux, on peut faire apparaître des scénarii inattendus. Après, effectivement, si j’en juge par ce qui circule, ça n’a pas encore trop pris. C’est marrant que l’auteur dise que ça va prendre, c’est ce que j’entendais il y a 10 ans. Mais tant que ça n’a pas totalement pris, difficile de dire autre chose 🙂 Un bémol favorable tout de même : il y a pas mal d’articles qui me semblent entrer dans cette catégorie qui ont quelques lettres de noblesse. Je pense, parmi d’autres, au El Farol Problem de Brian Arthur. Dans le domaine des interactions sociales, ces outils sont quand même assez impressionnants.
A propos des automates cellulaires (dont le modèle de Schelling est un exemplaire), le plus célèbre d’entre eux :
en.wikipedia.org/wiki/Con…
Le modèle de Schelling se classe dans les modèles multi-agents plutôt que dans les automates cellulaires.
Un autre lien vers un modèle de Schelling interactif : p.seppecher.free.fr/schel…
plus précisément suite à eric c – ce qui différencie les automates cellulaires de l’agent, en général, c’est la possibilité de faire varier son voisinage (agent) ou d’avoir un voisinage fixe (automate). le modèle de scelling est justement, pile, sur le sujet du changement de voisinage.