Dis Monsieur Solow, comment ça marche la croissance ?
Rédacteur : Stéphane Ménia
Cette présentation du modèle de Solow se base sur l'article de Solow de 1956 et intègre quelques remarques qui n'y figurent pas.
Fondamentaux de l’économie
L’économie produit un seul bien, qui sert de capital et de bien de consommation.
Deux facteurs (capital et travail) sont utilisés pour le produire.
La fonction de production est à facteurs substituables.
Il faut une quantité positive des deux facteurs pour pouvoir produire.
La productivité marginale des facteurs est positive et décroissante.
Les rendements d’échelle de la fonction de production sont constants :
Y = F(K,L)
F(0,L) = F(K,0) = 0
dF/dK > 0, dF/ dL > 0, d²F/dK² < 0, d²F/dL² < 0F(l K,l L) = l F(K,L)
Les rendements d’échelle constants permettent de réécrire la fonction de production en une fonction à un seul facteur, k = K/L, le capital par travailleur.
On obtient y = f (k), y = Y/L, le produit par travailleur.
Comportements et dynamique du modèle
On suppose que la population croît à un taux constant n :
L(t) = L0.exp(nt)
L’offre de travail est donc donnée et égale au travail utilisé pour produire le bien. Il y a plein-emploi.
Une partie de la production est épargnée. Elle est constante et égale à s.Y = s.f(k).
L’épargne est égale à l’investissement. s.Y = dK/dt. Ou encore : dk/dt = s.f(k) - n.k
Cette équation signifie que le capital nouveau (s.f(k)) est réparti entre la dotation aux nouveaux travailleurs (n.k) et un accroissement de la dotation de chacun des travailleurs (dk/dt).
Cette équation indique donc comment se fait l’accumulation du capital par travailleur. On en déduit l’évolution du produit par tête :
dy/dt = f ’(k).k
De sorte que la dynamique de l’économie est déterminée par celle du capital par tête.
Les conclusions de Solow sont qu’il existe un régime de croissance équilibrée de plein-emploi et que ce sentier est stable.
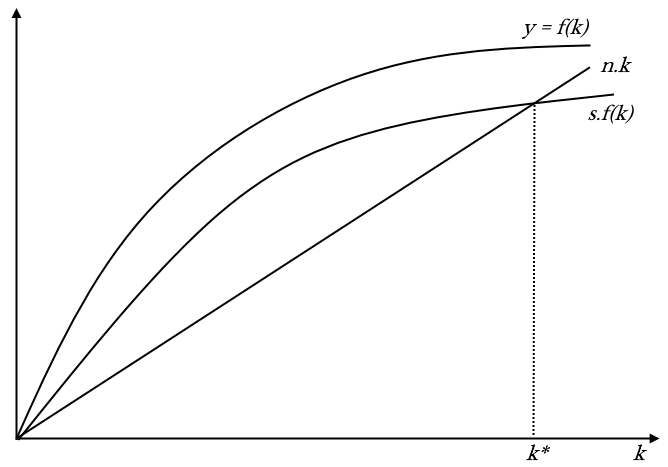
À l’équilibre stationnaire, le capital croît au même taux que le travail, soit n. L’équilibre stationnaire définit un capital par tête k* tel que dk/dt soit nul.
On a s.f(k) = n.k ou encore s.F(K,L) = n.K/L.
Si on prend une fonction Cobb-Douglas : Y = A.Ka L1-a
On a donc : s.A.Ka L1-a = n.K/L.
On en déduit le sentier de croissance équilibré : L = (s.A/n)1/(a-2)K(a-1)/(a-2).
Et on peut montrer que dK/K = dL/L = n.
Par ailleurs, on démontre facilement que ce sentier est stable. Partant d’un point où k est différent de k*, on aboutit toujours à k*. C’est à dire que le régime transitoire converge toujours vers l’équilibre stationnaire unique.
Si l’on part d’une situation où le stock de capital est faible, sa productivité marginale est élevée, l’incitation à investir est forte. Le ratio K/L augmente. La productivité marginale du capital diminue peu à peu alors que le taux de croissance augmente jusqu’à ce que la productivité marginale du capital s’annule. On retrouve l’état stationnaire. On peut tenir le raisonnement symétrique en cas de suraccumulation initiale.
La croissance équilibrée n’est pas un "fil du rasoir", puisque partant de n’importe quel rapport K/L, on converge vers un rapport d’équilibre.
Par ailleurs, la notion de déséquilibre n’est pas exclue, puisque dans le régime transitoire, le rapport K/L peut être différent de celui d’équilibre. Mais, il est, comme son nom l’indique, transitoire.
Dans ce modèle, la croissance du capital par tête et du produit par tête s’annule dans le long terme. Cela tient aux caractéristiques de la fonction de production. Les rendements sont constants et la productivité marginale du capital décroissante. Comme la population active croît à un taux constant, la seule façon d’accroître le produit par tête est d’accumuler toujours plus de capital. Or, sa productivité marginale est décroissante. Ce qui signifie que lorsque l’on l’accumule toujours plus, le produit marginal qui en est tiré est toujours plus petit. Il arrive un moment où il devient nul, et l’accumulation cesse.
Le modèle de Solow, dans ces conditions devient incapable de représenter une croissance de long terme du produit par tête.
L’introduction d’un progrès technique exogène
Solow envisage la prise en compte d’un progrès technique neutre. Il l’introduit dans la fonction de production sans l’affecter à un facteur en particulier. Il suppose simplement que :
Y = A.F(K,L).
A étant supposé de la forme A(t) = exp(g.t).
Il s’interprète comme un paramètre technologique qui accroît la production au cours du temps, de manière exogène. De sorte que le stock de capital croît au taux n + g/(1-a ) en régime transitoire classique, et K/L augmente à un taux g/(1-a ) au delà du point d’équilibre stationnaire classique. La croissance est alors infinie.
Les déviations du sentier d’équilibre
Solow lui-même estime que son hypothèse de stabilité et d’invariabilité du sentier de croissance équilibrée n’est valable que pour de petites variations autour de ce sentier. Dans sa conférence Nobel en 1987, il reconnaît qu’à son sens, lorsque les déviations sont conséquentes, les mécanismes de court terme, concernant notamment la demande, ont de fortes chances de modifier le profil de la croissance. Le sentier de croissance équilibrée ne serait que localement stable.
L’épargne et la croissance
Il est surprenant de constater que le taux d’épargne n’a pas d’influence sur le rythme de l’accumulation, mais uniquement sur le niveau d’équilibre du capital par tête et du produit par tête. Ce qui signifierait qu’il est indifférent d’épargner beaucoup ou peu en termes de croissance du capital par tête et que seul le rythme de progrès technique affecte le taux de croissance.
Annexe : représentation graphique de l’équilibre stationnaire