Comment établir un lien entre taux d'intérêt et investissement ?
Rédacteur : Stéphane Ménia
Le modèle néoclassique (I. Fisher, "The theory of interest", 1930)
La firme maximise son profit, sur deux périodes , sous contrainte de technologie (c’est à dire la fonction de production). Le profit est la différence entre les recettes de l’entreprise et ses coûts. Les recettes sont exprimées par le produit du prix du bien vendu et de la production (p.y). Les coûts sont les coûts d’utilisation des facteurs, à savoir le capital et le travail. On suppose ici que le coût du travail ( le salaire) ne varie pas.
Les coûts du capital sont le taux d’intérêt et le coût de la dépréciation du capital. La somme des deux représente ce que l’on appelle le coût d’usage du capital. Il est important de savoir que même si l’investissement est financé par autofinancement (sans emprunt), le taux d’intérêt doit être pris en compte, car il représente un coût d’opportunité de l’utilisation du capital (qui pourrait être placé au taux d’intérêt en vigueur).
Avec une représentation mathématique simple, le programme est le suivant. La firme maximise son profit actualisé sur deux périodes :
p.y1 - ( 1 + r ) I + p.y2 / ( 1 + r )
y1 est la production de la première période, avant l’investissement ;
y2 celle de la seconde période, après l’investissement ;
r le taux d’intérêt;
p.y1 représente les recettes de la première période ;
p.y2 / (1 + r ) les recettes actualisées de la seconde période ;
(1 + r) I est le coût de l’investissement.
On néglige les coûts liés au travail et ceux de la dépréciation du capital.
Si on prend une fonction de production simple y = Ka, où K est le capital et 0 < a < 1, l’élasticité de la production par rapport au capital, on peut alors reécrire y1 et y2 de la façon suivante :
y1 = K1a
y2 = a( K1 + I )
K1 est le stock de capital initial détenu par l’entreprise.
Aussi, le profit se réécrit :
p.K1a - ( 1 + r ) I + p.( K1 + I )a/( 1 + r)
En dérivant le profit par rapport à I, en annulant la dérivée trouvée, et en posant p = 1 , on déduit la fonction d’investissement suivante :
I = [ ( 1 + r)2 / a ] [1/(a-1)] - K1
Si on calcule dI / dr, on trouve une valeur négative, I décroît donc avec r.
Le résultat du calcul de maximisation montre alors que, à l’optimum, l’entreprise doit égaliser la productivité marginale du capital et le coût d’usage du capital. Cette propriété de l’optimum fait de l’investissement une fonction décroissante du coût d’usage du capital. En particulier, l’investissement décroît avec le taux d’intérêt.
La fonction d’investissement néoclassique a par conséquent la forme suivante :
I = I( r ), avec I’(r) < 0
L’efficacité marginale du capital : taux d’intérêt et investissement chez Keynes
On trouve chez Keynes une relation décroissante entre l’investissement privé et le taux d’intérêt. Mais Keynes utilise au préalable la notion d’efficacité marginale du capital pour expliquer cette relation.
L’efficacité marginale du capital se définit comme le taux de rendement interne d’un investissement, c’est à dire le taux d’actualisation qui annule sa valeur actuelle nette (V.A.N.).
Un rappel sur la notion de V.A.N. est utile. La V.A.N. est la différence entre les revenus actualisés futurs attendus de l’investissement et le coût de l’investissement. Mathématiquement, on l’écrira :
V.A.N. = - I + ( R0 + R1 /(1 + i) + R2 /( 1 + i ) 2 + R3 / ( 1+ i ) 3 ... Rn / ( 1 + i ) n )
Rt les revenus de l’investissement escomptés pour l’année t ;
I le coût initial de l’investissement ;
i le taux d’actualisation retenu.
L’efficacité marginale du capital est, d’après sa définition , le i qui est solution de l’équation V.A.N. = 0. Il sera noté i*.
On notera au passage que "l'efficacité marginale du capital" de Keynes correspond au TRI en théorie financière moderne.
Compte tenu de l’efficacité marginale comparée des différents investissements possibles à un moment donné dans une économie, on peut ranger les projets du plus rentable au moins rentable.

Classement des projets d’investissement selon leur efficacité marginale
Ensuite, les entrepreneurs comparent l’efficacité marginale des différents projets et le taux d’intérêt courant. Pour un projet donné, si le taux d’intérêt est plus faible que l’efficacité marginale de l’investissement, alors l’entrepreneur préfère investir que de placer son capital au taux du marché. Dans le cas contraire (taux d’intérêt supérieur), il ne réalise pas le projet. Ainsi, au niveau macroéconomique, plus le taux d’intérêt sera élevé, moins il y aura de projets d’investissement réalisés. On le voit sur la figure suivante. Pour un taux d’intérêt r°, seuls les deux derniers projets ne sont pas réalisés. Pour r*, supérieur à r°,
les projets 2 et 3 ne sont plus rentables. Pour r*, seul le projet 1 est réalisé.
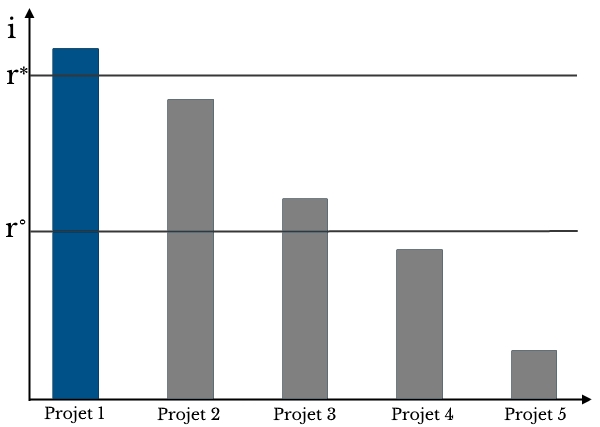
Variation du taux d’intérêt et réalisation des projets d’investissement.
L’investissement est donc une fonction décroissante du taux d’intérêt. La courbe correspondante est sensiblement la même que celle du modèle néoclassique. C’est un résultat énoncé par Keynes lui même. Cependant, on remarquera que dans l’expression de la V.A.N. qui détermine i, les Rt sont des revenus anticipés. Plus il seront élevés et plus l’efficacité marginale du capital sera élevée. On peut donc imaginer qu’en l’absence de variations du taux d’intérêt, l’investissement augmente ou diminue en fonction des anticipations des entrepreneurs. En particulier, en période de récession, il se peut que les anticipations de revenus futurs tirés de l’investissement soient si faibles que même un taux d’intérêt très bas ne permette pas une hausse de l’investissement.
En résumé, la liaison taux d’intérêt-investissement existe chez Keynes, mais elle disparaît si les opportunités d’investissement rentable dans l’économie sont peu nombreuses.
On le voit sur la figure qui suit, où malgré une diminution conséquente du taux d’intérêt de r* à r°, l’investissement ne varie pas.

Investissement et faiblesse des opportunités d’investir rentablement.